练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，直三棱柱中，，，，，点是棱上不同于的动点.

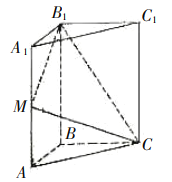
    （1）证明：；

    （2）若平面将棱柱分成体积相等的两部分，求此时二面角的余弦值.

    【答案】（1）见解析； （2）.

    【解析】

    （1）先由余弦定理可求得，再由勾股定理可得，然后由和即可证得平面，从而得证；

    （2）由题设知，，结合柱体的体积可得，所以是的中点，以为坐标原点，的方向为轴，轴，轴建立空间直角坐标系，进而利用法向量求解二面角即可.

    （1）证明：（方法一）在中，由余弦定理

    .

    ∴，则，∴.

    ∴，

    又，，

    ∴平面

    又平面，

    ∴

    证明：（方法二）在中，，

    ∴，∴

    又，，

    ∴平面

    又平面，

    ∴

    （2）

    由题设知，

    又

    ，∴是的中点.

    ∴以为坐标原点，的方向为轴，轴，轴建立如图的空间直角坐标，

    ∴，，，，，

    设是平面的法向量，

    ，，令，，

    ∴

    平面的法向量，

    .

    所以二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设,分别为椭圆:的左右焦点,已知椭圆上的点到焦点,的距离之和为4.

    (1)求椭圆的方程;

    (2)过点作直线交椭圆于,两点,线段的中点为,连结并延长交椭圆于点(为坐标原点),若,,等比数列,求线段的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把一颗骰子投掷2次，观察出现的点数，并记第一次出现的点数为，第二次出现的点数为，试就方程组解答下列各题：

    （1）求方程组只有一个解的概率；

    （2）求方程组只有正数解的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正四棱台中，，分别是的中点.

    （1）求证：平面平面；

    （2）求证：平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十七世纪法国数学家费马提出猜想：“当整数时，关于的方程没有正整数解”.经历三百多年，于二十世纪九十年中期由英国数学家安德鲁怀尔斯证明了费马猜想，使它终成费马大定理，则下面说法正确的是（ ）

    A. 存在至少一组正整数组使方程有解

    B. 关于的方程有正有理数解

    C. 关于的方程没有正有理数解

    D. 当整数时，关于的方程没有正实数解

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）求与椭圆有共同焦点且过点的双曲线的标准方程；

    （2）已知抛物线的焦点在轴上，抛物线上的点到焦点的距离等于5，求抛物线的标准方程和的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，底面，且，，，、分别是、的中点.

    (1)求证：平面平面；

    (2)求二面角的平面角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量，是平面内的一组基向量，为内的定点，对于内任意一点，当时，则称有序实数对为点的广义坐标，若点、的广义坐标分别为、，对于下列命题：

    ① 线段、的中点的广义坐标为；

    ② A、两点间的距离为；

    ③ 向量平行于向量的充要条件是；

    ④ 向量垂直于向量的充要条件是.

    其中的真命题是________（请写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两名射击运动员一次射击命中目标的概率分别是0.7，0.6，且每次射击命中与否相互之间没有影响，求：

    （1）甲射击三次，第三次才命中目标的概率；

    （2）甲、乙两人在第一次射击中至少有一人命中目标的概率；

    （3）甲、乙各射击两次，甲比乙命中目标的次数恰好多一次的概率.

    查看答案和解析>>

    同步练习册答案