
 已知,如图正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB,AD的中点.
已知,如图正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB,AD的中点.分析 (1)证明EF⊥平面ACG,即可证明EF⊥GH;
(2)作CM⊥HG交HG于点K,由两平面垂直的性质定理知CM⊥平面EFG,线段CM的长就是点C到平面EFG的距离,即可求点C到平面GEF的距离;
(3)BD和平面EFG的距离就是点B到平面EFG的距离.作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,即可求直线BD到平面GEF的距离.
解答 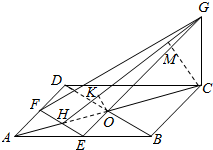 (1)证明:∵ABCD是正方形,
(1)证明:∵ABCD是正方形,
∴BD⊥AC,
∵E、F分别是AB,AD的中点,
∴EF∥BD,
∴EF⊥AC,
∵CG⊥平面ABCD,EF?平面ABCD,
∴EF⊥CG,
∵AC∩CG=C,
∴EF⊥平面ACG,
∵GH?平面ACG,
∴EF⊥GH
(2)解:∵EF?平面EFG,∴平面EFG⊥平面HCG,HG是这两个垂直平面的交线.
作CM⊥HG交HG于点K,由两平面垂直的性质定理知CM⊥平面EFG,
所以线段CM的长就是点C到平面EFG的距离.
∵正方形ABCD的边长为4,GC=2,
∴AC=4$\sqrt{2}$,HO=$\sqrt{2}$,HC=3$\sqrt{2}$.
∴在Rt△HCG中,HG=$\sqrt{22}$
∴CM=$\frac{2×3\sqrt{2}}{\sqrt{22}}$=$\frac{6\sqrt{11}}{11}$.
即点C到平面EFG的距离为$\frac{6\sqrt{11}}{11}$;
(3)解:连接EG、FG、EF、BD、AC、EF、BD分别交AC于H、O.
因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
由直线和平面平行的判定定理知BD∥平面EFG,
所以BD和平面EFG的距离就是点B到平面EFG的距离.
作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,
∴线段OK的长就是点B到平面EFG的距离.
∴点B到平面EFG的距离为OK=$\frac{2\sqrt{11}}{11}$.
点评 本题考查线面垂直的判定与性质,考查点面距离的计算能力,属于中档题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
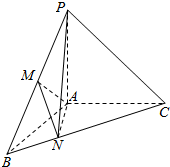 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
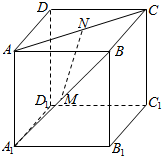 如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
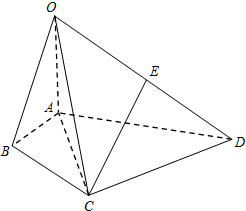 如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.
如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
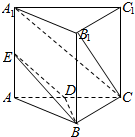 已知正三棱柱ABC-A1B1C1中,AB=2,AA1=$\sqrt{3}$,点D为AC的中点,点E在线段AA1上.
已知正三棱柱ABC-A1B1C1中,AB=2,AA1=$\sqrt{3}$,点D为AC的中点,点E在线段AA1上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
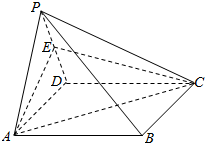 已知四棱锥P-ABCD的底面ABCD是矩形,PD⊥底面ABCD,E为棱PD的中点.
已知四棱锥P-ABCD的底面ABCD是矩形,PD⊥底面ABCD,E为棱PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
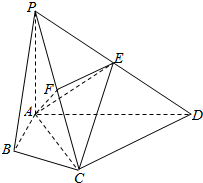 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com