
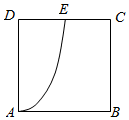
 如图,已知四边形ABCD是一块边长为2千米的正方形地皮,其中曲边三角形ADE是一个小池塘,点E在边CD上且DE=1千米.假设曲边AE可用以A为顶点,AD为对称轴的抛物线拟合,现绿化部门拟过曲边AE上一点P作切线交边AB于点M,交CD于点N,在四边形MBCN内栽种花草.
如图,已知四边形ABCD是一块边长为2千米的正方形地皮,其中曲边三角形ADE是一个小池塘,点E在边CD上且DE=1千米.假设曲边AE可用以A为顶点,AD为对称轴的抛物线拟合,现绿化部门拟过曲边AE上一点P作切线交边AB于点M,交CD于点N,在四边形MBCN内栽种花草.分析 (1)以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系.设抛物线的方程为y=ax2,代入E(1,2),可得抛物线的方程,求得导数,切线的斜率可得切线的方程,分别令y=0,y=2,可得M,N的坐标及MB,NC,由切线过C(2,2),可得t,由梯形的面积公式化简即可得到所求S(T);
(2)运用基本不等式:a+b≥2$\sqrt{ab}$(当且仅当a=b取得等号),即可得到所求面积的最大值.
解答 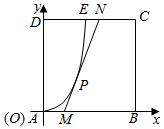 解:(1)以A为坐标原点,AB所在直线为x轴,
解:(1)以A为坐标原点,AB所在直线为x轴,
AD所在直线为y轴,建立直角坐标系.
设抛物线的方程为y=ax2,
由E(1,2)在抛物线上,可得a=2,
即有抛物线的方程为y=2x2,
导数为y′=4x,可得切线MN的斜率为4t,
切线的方程为y-2t2=4t(x-t),
令y=0,可得x=$\frac{t}{2}$,即有MB=2-$\frac{t}{2}$;
令y=2,可得x=$\frac{1}{2t}$+$\frac{t}{2}$,即NC=2-$\frac{1}{2t}$-$\frac{t}{2}$;
当切线经过点C(2,2),可得2-2t2=4t(2-t),
解得t=2-$\sqrt{3}$,
则S(t)=$\frac{1}{2}$×2(MB+NC)=4-$\frac{1}{2t}$-t(2-$\sqrt{3}$<t≤1);
(2)当2-$\sqrt{3}$<t≤1时,S(t)=4-$\frac{1}{2t}$-t
=4-($\frac{1}{2t}$+t)≤4-2$\sqrt{\frac{1}{2t}•t}$=4-$\sqrt{2}$.
当且仅当$\frac{1}{2t}$=t,即t=$\frac{\sqrt{2}}{2}$∈(2-$\sqrt{3}$,1]时,
S(t)取得最大值4-$\sqrt{2}$.
点评 本题考查四边形面积的解析式和最值的求法,注意运用基本不等式,同时考查导数的运用:求切线的方程,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com