
分析 (1)设出M点的坐标,由M为线段PD的中点得到P的坐标,把P的坐标代入y2=16x整理得线段PD的中点M的轨迹.
(2)设直线l的方程为x=my+1,代入抛物线方程,利用韦达定理,即可得出结论.
解答 解:(1))设M(x,y),由题意D(x,0),P(x,y1)
∵M为线段PD的中点,∴y1+0=2y,y1=2y.
又∵P(x,y1)在y2=16x上,∴y12=16x,
∴4y2=16x,即y2=4x.
(2)设直线l的方程为x=my+1,代入抛物线方程,可得:y2-4my-4=0
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4,
∴△AOB的面积=$\frac{1}{2}$|OF||y1-y2|=$\frac{1}{2}×1×\sqrt{16{m}^{2}+16}$≥2,m=0时取等号,
∴m=0时,△AOB的面积最小值为2.
点评 本题考查了轨迹方程的求法,训练了利用代入法求曲线的方程,考查直线与圆锥曲线的综合问题,考查学生分析解决问题的能力,是中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正六棱锥S-ABCDEF的底面边长为2,高为1,现从该棱锥的7个顶点中随机取3个点构成三角形,设随机变量X表示所得的三角形的面积.
已知正六棱锥S-ABCDEF的底面边长为2,高为1,现从该棱锥的7个顶点中随机取3个点构成三角形,设随机变量X表示所得的三角形的面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
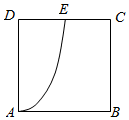 如图,已知四边形ABCD是一块边长为2千米的正方形地皮,其中曲边三角形ADE是一个小池塘,点E在边CD上且DE=1千米.假设曲边AE可用以A为顶点,AD为对称轴的抛物线拟合,现绿化部门拟过曲边AE上一点P作切线交边AB于点M,交CD于点N,在四边形MBCN内栽种花草.
如图,已知四边形ABCD是一块边长为2千米的正方形地皮,其中曲边三角形ADE是一个小池塘,点E在边CD上且DE=1千米.假设曲边AE可用以A为顶点,AD为对称轴的抛物线拟合,现绿化部门拟过曲边AE上一点P作切线交边AB于点M,交CD于点N,在四边形MBCN内栽种花草.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤2} | B. | {x|0<x<2} | C. | {0,1,2} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com