
 已知正六棱锥S-ABCDEF的底面边长为2,高为1,现从该棱锥的7个顶点中随机取3个点构成三角形,设随机变量X表示所得的三角形的面积.
已知正六棱锥S-ABCDEF的底面边长为2,高为1,现从该棱锥的7个顶点中随机取3个点构成三角形,设随机变量X表示所得的三角形的面积.分析 (1)从7个顶点中随机选取3个点构成三角形,共有${C}_{7}^{3}$=35种取法,求出X=$\sqrt{3}$的三角形的个数,由此能求出P(X=$\sqrt{3}$).
(2)由题意,X的可能取值为$\sqrt{3}$,2,$\sqrt{6}$,2$\sqrt{3}$,3$\sqrt{3}$,分别求出相应的概率,由此能求出随机变量X的概率分布列和E(X).
解答 解:(1)从7个顶点中随机选取3个点构成三角形,
共有${C}_{7}^{3}$=35种取法,其中X=$\sqrt{3}$的三角形如△ABF,
这类三角形共有6个,
∴P(X=$\sqrt{3}$)=$\frac{6}{{C}_{7}^{3}}$=$\frac{6}{35}$.
(2)由题意,X的可能取值为$\sqrt{3}$,2,$\sqrt{6}$,2$\sqrt{3}$,3$\sqrt{3}$,
其中,X=$\sqrt{3}$的三角形如△ABF,这类三角形共有6个,
其中,X=2的三角形有两类,如△SAD(3个),△SAB(6个),共9个,
其中X=$\sqrt{6}$的三角形如△SBD,这类三角形共有6个,
其中X=2$\sqrt{3}$的三角形如△CDF,这类三角形共有12个,
其中X=3$\sqrt{3}$的三角形如△BDF,这类三角形共有2个,
∴P(X=$\sqrt{3}$)=$\frac{6}{35}$,P(X=2)=$\frac{9}{35}$,
P(X=$\sqrt{6}$)=$\frac{6}{35}$,P(X=2$\sqrt{3}$)=$\frac{12}{35}$,
P(X=3$\sqrt{3}$)=$\frac{2}{35}$,
随机变量X的概率分布列为:
| X | $\sqrt{3}$ | 2 | $\sqrt{6}$ | 2$\sqrt{3}$ | 3$\sqrt{3}$ |
| P | $\frac{6}{35}$ | $\frac{9}{35}$ | $\frac{6}{35}$ | $\frac{12}{35}$ | $\frac{2}{35}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
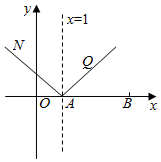 在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.
在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com