
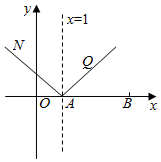 在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.
在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.分析 (Ⅰ)由已知条件,设点M坐标,代入|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|,化简即可得动点M的轨迹E的方程;
(Ⅱ)射线AQ与射线AN关于直线x=1对称,证明kQA+kNA=0即可.
解答 (Ⅰ)解:设M(x,y),$|{\overrightarrow{BM}}|=\sqrt{{{(x-4)}^2}+{y^2}}$,$|{\overrightarrow{AM}}|=\sqrt{{{(x-1)}^2}+{y^2}}$,
由于$|{\overrightarrow{BM}}|=2|{\overrightarrow{AM}}|$,则$\sqrt{{{(x-4)}^2}+{y^2}}$=$2\sqrt{{{(x-1)}^2}+{y^2}}$,
化简得,x2+y2=4,
动点M的轨迹E的方程x2+y2=4.-------(4分)
(Ⅱ)证明:设Q(x1,y1),N(x2,y2),直线l:y=k(x-4),
联立$\left\{\begin{array}{l}{x^2}+{y^2}=4\\ y=k(x-4)\end{array}\right.$,得(1+k2)x2-8k2x+16k2-4=0,
判别式△=16(1-3k2)>0,解之:$-\frac{{\sqrt{3}}}{3}<k<\frac{{\sqrt{3}}}{3}$,${x_1}+{x_2}=\frac{{8{k^2}}}{{1+{k^2}}}$,${x_1}{x_2}=\frac{{16{k^2}-4}}{{1+{k^2}}}$,
又因为y1=k(x1-4),y2=k(x2-4),kQA+kNA=$\frac{y_1}{{{x_1}-1}}+\frac{y_2}{{{x_2}-1}}$=$\frac{{k({x_1}-4)({x_2}-1)+k({x_2}-4)({x_1}-1)}}{{({x_1}-1)({x_2}-1)}}$
=$k\frac{{2{x_1}{x_2}-5({x_1}+{x_2})+8}}{{({x_1}-1)({x_2}-1)}}$,
由于2x1x2-5(x1+x2)+8=$2•\frac{{16{k^2}-4}}{{1+{k^2}}}$$-5•\frac{{8{k^2}}}{{1+{k^2}}}$+$8•\frac{{1+{k^2}}}{{1+{k^2}}}$=0,
所以,kQA+kNA=0,即,kQA=-kNA,
因此,射线AQ与射线AN关于直线x=1对称.-----------(12分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,设D是图中所示的矩形区域,E是D内函数y=cosx图象上方的点构成的区域.向D中随机投一点,则该点落入E(阴影部分)中的概率为$\frac{π-2}{π}$.
如图,设D是图中所示的矩形区域,E是D内函数y=cosx图象上方的点构成的区域.向D中随机投一点,则该点落入E(阴影部分)中的概率为$\frac{π-2}{π}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正六棱锥S-ABCDEF的底面边长为2,高为1,现从该棱锥的7个顶点中随机取3个点构成三角形,设随机变量X表示所得的三角形的面积.
已知正六棱锥S-ABCDEF的底面边长为2,高为1,现从该棱锥的7个顶点中随机取3个点构成三角形,设随机变量X表示所得的三角形的面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤2} | B. | {x|0<x<2} | C. | {0,1,2} | D. | {0,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com