练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．函数y=x-lnx的单调减区间为（　　）
    A．（0，1）B．（1，2）C．（-∞，-1）D．（-∞，-1）和（1，+∞）

    分析 求出函数的导数，通过导数小于0求出x的范围，即可得到函数的单调减区间．

    解答 解：由y=x-lnx，得$y'=1-\frac{1}{x}=\frac{x-1}{x}＜0$，即0＜x＜1，
    故选：A．

    点评 本题考查函数的导数与单调性的关系，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．过点（2，0）引直线l与圆x2+y2=2相交于A，B两点，O为坐标原点，当△AOB面积取最大值时，直线l的斜率为±$\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．空间中，可以确定一个平面的条件是（　　）
    A．三个点B．四个点C．三角形D．四边形

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．设离散型随机变量X的所有可能值为1，2，3，4，且P（x=k）=ak，（k=1，2，3，4）
    （1）求常数a的值；
    （2）求X的分布列；
    （3）求P（2≤x＜4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．高三年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如频率分布表：
    分组频数（ni）频率（fi）
    [85，95）①
    [95，105）0.050
    [105，115）0.200
    [115，125）120.300
    [125，135）0.275
    [135，145）4
    [145，155]0.050
    合计
    根据图表，①处的数值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

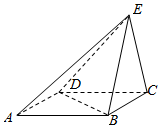    13．已知四棱锥E-ABCD的底面是平行四边形，BC=2，BD=$\sqrt{6}$，ED=4，EB=EC=$\sqrt{10}$，平面BCE⊥平面ABCD．
    （Ⅰ）证明：BD⊥平面EBC；
    （Ⅱ）求三棱锥B-ADE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．用数学归纳法证明：2n+2•3n+5n-4（n∈N*）能被25整除．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设{an}是等差数列，数列{an}的前n项和为Sn，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b2=7，S2+b2=6
    （Ⅰ）求{an}，{bn}的通项公式；
    （Ⅱ）求数列{an•bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

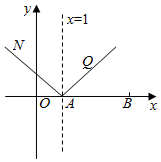    18．在直角坐标平面内，已知两点A（1，0），B（4，0），设M是平面内的动点，并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|．
    （Ⅰ）求动点M的轨迹E的方程；
    （Ⅱ）自点B引直线l交曲线E于Q，N两点，求证：射线AQ与射线AN关于直线x=1对称．

    查看答案和解析>>

    同步练习册答案