
分析 根据条件判断函数的周期性,利用函数奇偶性和周期性的关系进行转化求解即可
解答 解:∵设f(x)是定义在R上的奇函数,且对任意实数x都有f(x+3)=f(-x)=-f(x),
∴f(x+6)=-f(x+3)=f(x),
∴函数f(x)是周期为6的周期函数,
∵当x∈[0,2]时,f(x)=x2-4x,
∴f(0)=0,f(1)=2-1=1,f(2)=0,f(3)=-1,
∴f(2015)=f(335×6+5)=f(5)=-f(-5)-f(-5+6)=-f(1)=-3
f(2016)=f(6×336)=f(0)=0,
f(2015)+f(2016)=-3+0=-3
故答案为:-3
点评 本题主要考查函数值的计算,根据条件判断函数的周期性是解决本题的关键.


科目:高中数学 来源: 题型:解答题
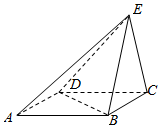 已知四棱锥E-ABCD的底面是平行四边形,BC=2,BD=$\sqrt{6}$,ED=4,EB=EC=$\sqrt{10}$,平面BCE⊥平面ABCD.
已知四棱锥E-ABCD的底面是平行四边形,BC=2,BD=$\sqrt{6}$,ED=4,EB=EC=$\sqrt{10}$,平面BCE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
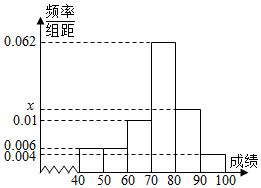 某班50名学生的数学成绩的频率分布直方图如图:
某班50名学生的数学成绩的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
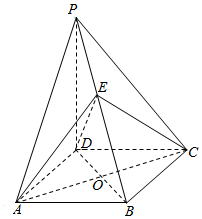 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=PD=2,O为AC与BD的交点,E为棱PB上一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=PD=2,O为AC与BD的交点,E为棱PB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
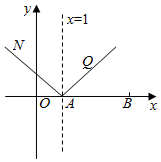 在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.
在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 55 | B. | 52 | C. | 39 | D. | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com