
分析 利用辅助角公式化简函数的解析式,再利用余弦函数的定义域和值域,求得函数的值域.
解答 解:(1)函数f(x)=cosx-$\sqrt{3}$sinx=2($\frac{1}{2}$cosx-$\frac{\sqrt{3}}{2}$sinx)=2cos(x+$\frac{π}{3}$).
(2)函数f(x)=2cos(x+$\frac{π}{3}$)∈[-2,2],即f(x)的值域为[-2,2].
(3)当x∈[0,$\frac{π}{2}$]时,x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],∴cos(x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$],
∴f(x)=2cos(x+$\frac{π}{3}$)的值域为[-$\sqrt{3}$,1].
点评 本题主要考查辅助角公式,余弦函数的定义域和值域,属于基础题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
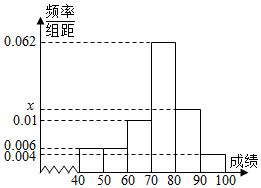 某班50名学生的数学成绩的频率分布直方图如图:
某班50名学生的数学成绩的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.
在直角坐标平面内,已知两点A(1,0),B(4,0),设M是平面内的动点,并且|${\overrightarrow{BM}}$|=2|${\overrightarrow{AM}}$|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com