Question

17£®¹ýË«ÇúÏß$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1£¨a£¾0£¬b£¾0£©µÄÓÒ½¹µãF₂£¨c£¬0£©×÷Ô²x²+y²=a²µÄÇÐÏߣ¬ÇеãΪM£¬ÑÓ³¤F₂M½»Å×ÎïÏßy²=-4cxÓÚµãP£¬ÆäÖÐOΪ×ø±êÔ­µã£¬Èô$\overrightarrow{OM}=\frac{1}{2}£¨\overrightarrow{O{F_2}}+\overrightarrow{OP}£©$£¬ÔòË«ÇúÏßµÄÀëÐÄÂÊΪ£¨¡¡¡¡£©

• A£® $\frac{4\sqrt{2}-2}{7}$
• B£® $\frac{4\sqrt{2}+2}{7}$
• C£® $\frac{1+\sqrt{3}}{2}$
• D£® $\frac{1+\sqrt{5}}{2}$

Answer 1

·ÖÎö ˵Ã÷MÊÇF₂PµÄÖе㣮ÉèÅ×ÎïÏߵĽ¹µãΪF₁£¬ÔòF₁Ϊ£¨-c£¬0£©£¬Ò²ÊÇË«ÇúÏߵĽ¹µã£®»­³öͼÐΣ¬Á¬½ÓPF₁£¬OM£¬ËµÃ÷OMΪ¡÷PF₂F₁µÄÖÐλÏߣ®Í¨¹ýPF₂¡ÍPF₁£¬¿ÉµÃ|PF₂|=$\sqrt{4{c}^{2}-4{a}^{2}}=2b$£¬ÉèP£¨x£¬y£©£¬ÍƳö c-x=2a£¬ÀûÓÃË«ÇúÏ߶¨Òå½áºÏ¹´¹É¶¨ÀíµÃ y²+4a²=4b²£¬È»ºóÇó½âÀëÐÄÂʼ´¿É£®

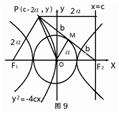½â´ð ½â£ºÈçͼ9£¬¡ß$\overrightarrow{OM}=\frac{1}{2}£¨\overrightarrow{O{F_2}}+\overrightarrow{OP}£©$£¬¡àMÊÇF₂PµÄÖе㣮
ÉèÅ×ÎïÏߵĽ¹µãΪF₁£¬ÔòF₁Ϊ£¨-c£¬0£©£¬Ò²ÊÇË«ÇúÏߵĽ¹µã£®
Á¬½ÓPF₁£¬OM£®¡ßO¡¢M·Ö±ðÊÇF₁F₂ºÍPF₂µÄÖе㣬¡àOMΪ
¡÷PF₂F₁µÄÖÐλÏߣ®¡ßOM=a£¬¡à|PF₁|=2 a£®¡ßOM¡ÍPF₂£¬
¡àPF₂¡ÍPF₁£¬ÓÚÊǿɵÃ|PF₂|=$\sqrt{4{c}^{2}-4{a}^{2}}=2b$£¬ÉèP£¨x£¬y£©£¬Ôò c-x=2a£¬
ÓÚÊÇÓÐx=c-2a£¬y²=-4c£¨c-2 a£©£¬¹ýµãF₂×÷xÖáµÄ´¹Ïߣ¬µãPµ½¸Ã´¹ÏߵľàÀëΪ2a£®
Óɹ´¹É¶¨ÀíµÃ y²+4a²=4b²£¬¼´-4c£¨c-2a£©+4 a²=4£¨c²-a²£©£¬
±äÐοɵÃc²-a²=ac£¬Á½±ßͬ³ýÒÔa²
ÓРe²-e-1=0£¬ËùÒÔe=$\frac{1+\sqrt{5}}{2}$£¬¸ºÖµÒѾ­ÉáÈ¥£®
¹ÊÑ¡£ºD£®

µãÆÀ ±¾Ì⿼²éË«ÇúÏߵļòµ¥ÐÔÖʵÄÓ¦Óã¬ÏòÁ¿ÒÔ¼°Ô²ÓëË«ÇúÏßµÄλÖùØϵµÄ×ÛºÏÓ¦Ó㬿¼²éת»¯Ë¼ÏëÒÔ¼°¼ÆËãÄÜÁ¦£®