分析:由题意作出平面区域,
(1)化z=x-2y为y=
x-
,-
是y=
x-
的截距,从而解得;
(2)z=x+7y与x+7y-11=0平行,故z=x+7y的最大值为11;
(3)x
2+y
2的几何意义是阴影内的点到原点的距离的平方,从而求解;
(4)
=2
的几何意义是阴影内的点与(-4,-7)连线的直线的斜率的2倍,从而求解;
(5)z=|x+2y+20|的几何意义是阴影内的点到直线x+2y+20=0的距离的
倍;从而求解;
(6)
=(2,1);
=(x,y);|
|cos∠MOP=
=
(2x+y);从而求解.
解答:
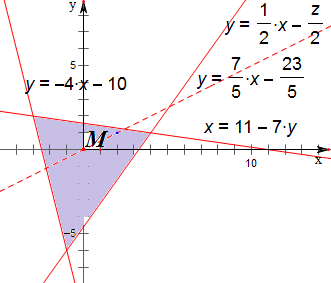
解:由题意作出平面区域,
(1)化z=x-2y为y=
x-
,-
是y=
x-
的截距,
故由
解得,
x=-1,y=-6;
此时z=x-2y取得最大值-1+12=11;
(2)z=x+7y与x+7y-11=0平行,
故z=x+7y的最大值为11;
(3)x
2+y
2的几何意义是阴影内的点到原点的距离的平方,
故其最大值为(-1)
2+(-6)
2=37;
(4)
=2
的几何意义是阴影内的点与(-4,-7)连线的直线的斜率的2倍;
≤
≤
;
即
≤
≤9,
故
的取值范围为[
,18];
(5)z=|x+2y+20|的几何意义是阴影内的点到直线x+2y+20=0的距离的
倍;
由图象可得,阴影内的点到直线x+2y+20=0的最小距离为

d=
=
;
故z=|x+2y+20|的最小值为7;
(6)
=(2,1);
=(x,y);
|
|cos∠MOP=
=
(2x+y);
则当x=-1,y=-6时有最小值,
|
|cos∠MOP的最小值为
(-2-6)=-
.

 解:由题意作出平面区域,
解:由题意作出平面区域,


 名校课堂系列答案
名校课堂系列答案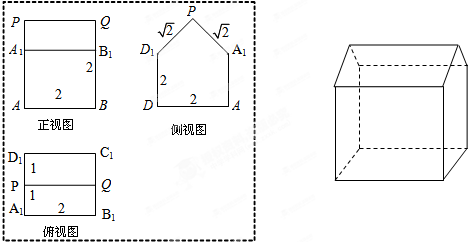
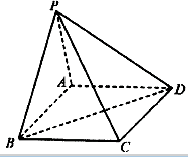 如图,在四棱锥P-ABCD中,底面ABCD是正方形,已知AB=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是正方形,已知AB=2,PA=2,PD=2