
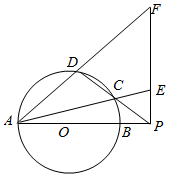
 如图,AB为圆O的直径,P是AB延长线上一点,割线PCD交圆O于C,D两点,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,AB为圆O的直径,P是AB延长线上一点,割线PCD交圆O于C,D两点,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.分析 (1)连接BD,由对应角相等可得△ADB∽△APF,由相似三角形的性质和四点共圆的判定:对角互补,即可得证;
(2)由圆的割线定理可得,PB•PA=PC•PD,结合条件求得PD,OD,连接OD,在△POD中运用余弦定理,可得cos∠DPO,再由诱导公式即可得到所求值.
解答 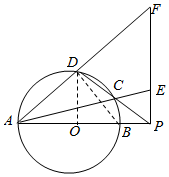 解:(1)证明:连接BD,
解:(1)证明:连接BD,
由AB为直径,可得∠ADB=90°,
由∠APF=∠ADB=90°,
且∠DAB=∠PAF,
可得△ADB∽△APF,
即有∠ABD=∠AFP,
又∠ACD=∠ABD,
可得∠ACD=∠AFP,
即∠DCE+∠DFE=180°,
可得F、E、C、D四点共圆;
(2)AP=10,BP=2,CP=3,
由圆的割线定理可得,PB•PA=PC•PD,
即为2×10=3PD,
即PD=$\frac{20}{3}$.
PA=PB+AB,即AB=PA-PB=10-2=8.
可得OD=4,
连接OD,在△POD中,PO=6,PD=$\frac{20}{3}$,OD=4,
由余弦定理可得cos∠DPO=$\frac{P{D}^{2}+P{O}^{2}-O{D}^{2}}{2PD•PO}$
=$\frac{\frac{400}{9}+36-16}{2×\frac{20}{3}×6}$=$\frac{29}{36}$.
则sin∠DPF=sin(90°-∠DPO)=cos∠DPO=$\frac{29}{36}$.
点评 本题考查圆的割线定理和相似三角形的判定和性质,考查四点共圆的判定,注意运用对角互补,考查推理能力和运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
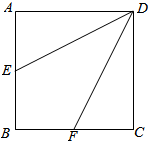 如图,在正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P,点P在平面DEF上的射影点为H.
如图,在正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P,点P在平面DEF上的射影点为H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$)及(0,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,0)及($\frac{1}{2}$,+∞) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
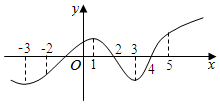
| A. | 在区间(1,3)内f(x)是减函数 | B. | 当x=1时,f(x)取到极大值 | ||
| C. | 在(4,5)内f(x)是增函数 | D. | 当x=2时,f(x)取到极小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com