
分析 求导,根据题意可知导函数f′(x)不存在变号的零点,令f′(x)=0,则-2m=$\frac{lnx+1}{x}$,构造辅助函数g(x)=$\frac{lnx+1}{x}$,(x>0),求导,利用导数求得函数的最大值,即可求得实数m的取值范围.
解答 解:f′(x)=lnx+1+2mx,
故函数f′(x)不存在变号的零点,
令f′(x)=0,即lnx+1+2mx=0,
则-2m=$\frac{lnx+1}{x}$,设g(x)=$\frac{lnx+1}{x}$,(x>0),
g′(x)=$\frac{-lnx}{{x}^{2}}$,(x>0),
令g′(x)=0,解得x=1,
当x在(0,1),g′(x)>0,函数单调递增,
当x在(1,+∞),g′(x)<0,函数单调递减,
∴当x=1函数g(x)取极大值,即函数的最大值,无最小值,
故想要f′(x)不存在变号的零点,即-2m≥1,即m≤-$\frac{1}{2}$,
则m的取值范围为(-∞,-$\frac{1}{2}$].
故答案为:(-∞,-$\frac{1}{2}$].
点评 本题考查利用导数求函数的单调性、极值及最值,着重考查恒成立问题,考查构造函数与方程的数学思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{{8\sqrt{5}}}{5}$ | C. | $\frac{{16\sqrt{5}}}{5}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a2+a3-a1,b2+b3-b1) | B. | (b2+b3-b1,a2+a3-a1) | ||
| C. | (a2+a3-2a1,b2+b3-2b1) | D. | (b2+b3-2b1,a2+a3-2a1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
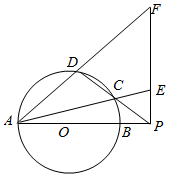 如图,AB为圆O的直径,P是AB延长线上一点,割线PCD交圆O于C,D两点,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,AB为圆O的直径,P是AB延长线上一点,割线PCD交圆O于C,D两点,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
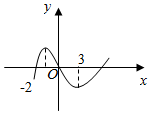 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=lnf′(x)的单调减区间为( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=lnf′(x)的单调减区间为( )| A. | [0,3) | B. | [-2,3] | C. | (-∞,-2) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com