
分析 两条直线l1:3x+4y-2=0与l2:2x+y+2=0的方程联立可得交点P.
(1)利用点斜式即可得出.
(2)由直线m与直线l平行,可设直线m的方程为x+y+C=0,由点到直线的距离公式可得C.
解答 解:由$\left\{\begin{array}{l}{3x+4y-2=0}\\{2x+y+2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,∴点P的坐标是(-2,2),
(1)k=$\frac{2}{-2}$=-1,可得所求直线方程为y=-x.
(2)由直线m与直线l平行,可设直线m的方程为x+y+C=0,由点到直线的距离公式得$\frac{|-2+2+c|}{\sqrt{2}}$=3,解得c=$±3\sqrt{2}$,故所求直线方程为x+y+3$\sqrt{2}$=0或x+y-3$\sqrt{2}$=0.
点评 本题考查了相互平行的直线斜率之间的关系、点到直线的距离公式、直线的交点坐标,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图直角梯形OABC中,$∠COA=∠OAB=\frac{π}{2},OC=2,OA=AB=1,SO⊥$面OABC,SO=1,以OC,OA,OS分别为x轴,y轴,z轴建立直角坐标系O-xyz.
如图直角梯形OABC中,$∠COA=∠OAB=\frac{π}{2},OC=2,OA=AB=1,SO⊥$面OABC,SO=1,以OC,OA,OS分别为x轴,y轴,z轴建立直角坐标系O-xyz.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
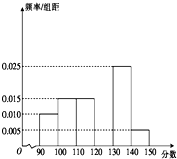 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )| A. | 121 | B. | 119 | C. | 118.5 | D. | 118 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {-1,1} | C. | {0,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①、②、③均直线 | B. | 只有②是直线 | C. | ①、②是直线,③是圆 | D. | ②是直线,①、③是圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com