
分析 设两个课外活动小组都参加的人有x人,建立文氏图,得到15+(32-x)+(24-x)+x=54,求出x=17,有此能求出从该班中任意抽取1名同学,他参加了两个课外活动小组的概率.
解答 解: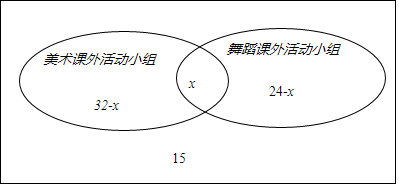 v某班54个学生中,参加美术课外活动小组的有32人,
v某班54个学生中,参加美术课外活动小组的有32人,
参加舞蹈课外活动小组的有24人,这两个课外活动小组都没有参加的有15人,
设两个课外活动小组都参加的人有x人,
如图,建立文氏图,
∴15+(32-x)+(24-x)+x=54,
解得x=17,
∴从该班中任意抽取1名同学,他参加了两个课外活动小组的概率是p=$\frac{17}{54}$.
点评 本题考查概率的求法,考查古典概型、集合等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想,是基础题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com