
分析 (1)根据对数函数成立的条件建立不等式关系即可求出函数的定义域.
(2)根据函数奇偶性的定义进行判断即可.
(3)利用函数单调性的定义进行判断和证明即可.
解答 解:(1)由1-x2>0得-1<x<1,即函数的定义域为(-1,1);
(2)∵f(-x)=log${\;}_{\sqrt{2}}$(1-x2)=f(x),
∴函数f(x)为偶函数;
(3)设0<x1<x2<1,
则f(x1)-f(x2)=log${\;}_{\sqrt{2}}$(1-x12)-log${\;}_{\sqrt{2}}$(1-x22)=log${\;}_{\sqrt{2}}$($\frac{1-{{x}_{1}}^{2}}{1-{{x}_{2}}^{2}}$)
∵0<x1<x2<1,∴0<x12<x22<1,
即-x12>-x22>-1,
即1-x12>1-x22>0,
则$\frac{1-{{x}_{1}}^{2}}{1-{{x}_{2}}^{2}}$>1,即f(x1)-f(x2)=log${\;}_{\sqrt{2}}$($\frac{1-{{x}_{1}}^{2}}{1-{{x}_{2}}^{2}}$)>0,
即f(x1)>f(x2),
即函数在(0,1)上的单调递减.
点评 本题主要考查函数定义域,函数奇偶性和单调性的判断和证明,利用定义法是解决本题的关键.


科目:高中数学 来源: 题型:填空题
 如图,已知正三角形ABC内接于半径为2的圆O,E为线段BC上一动点,延长AE交圆O于点F,则$\overrightarrow{FA}$•$\overrightarrow{FB}$的取值范围是[-6,0].
如图,已知正三角形ABC内接于半径为2的圆O,E为线段BC上一动点,延长AE交圆O于点F,则$\overrightarrow{FA}$•$\overrightarrow{FB}$的取值范围是[-6,0].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和② | B. | ①和③ | C. | ②和④ | D. | ①和④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
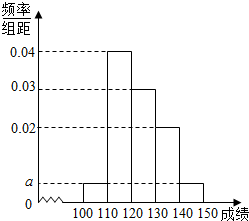 贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].| 分数段 | [100,110) | [110,120) | [120,130) | [130,140) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com