
已知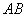 是圆柱底面圆的直径,
是圆柱底面圆的直径, 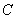 是底面圆周上异于
是底面圆周上异于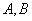 的任意一点,母线
的任意一点,母线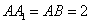 ;
;
(1)求证: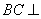 平面
平面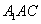 ;(2)求三棱锥
;(2)求三棱锥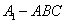 的体积的最大值.
的体积的最大值.
(1)∵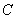 是底面圆周上异于
是底面圆周上异于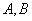 的任意一点,
的任意一点,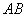 是圆柱底面圆的直径,
是圆柱底面圆的直径,
∴BC⊥AC, ∵AA1⊥平面ABC,BCÌ平面ABC,∴AA1⊥BC,
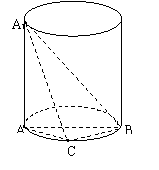 ∵AA1∩AC=A,AA1Ì平面AA1 C,ACÌ平面AA1 C,
∵AA1∩AC=A,AA1Ì平面AA1 C,ACÌ平面AA1 C,
∴BC⊥平面AA1C.
(2)解法1:设AC=x,在Rt△ABC中,
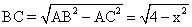 (0<x<2)
(0<x<2)
故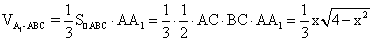 (0<x<2),
(0<x<2),
即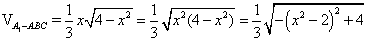 .
.
∵0<x<2,0<x2<4,∴当x2=2,即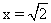 时,三棱锥A1-ABC的体积的最大值为
时,三棱锥A1-ABC的体积的最大值为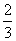
.解法2: 在Rt△ABC中,AC2+BC2=AB2=4,
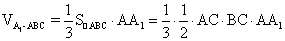
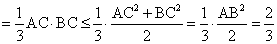 .
.
当且仅当 AC=BC 时等号成立,此时AC=BC=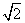 .
.
解法3:设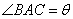 ,则在Rt△ABC中,
,则在Rt△ABC中,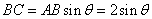 ,
,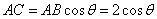
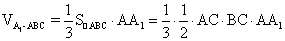
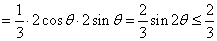 .
.
当且仅当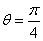 即 AC=BC 时等号成立,此时AC=BC=
即 AC=BC 时等号成立,此时AC=BC=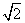 .
.


科目:高中数学 来源: 题型:
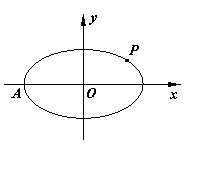
椭圆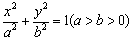 的离心率为
的离心率为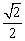 , 过点
, 过点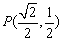 , 记椭圆的左顶点为
, 记椭圆的左顶点为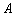 .
.
(1)求椭圆的方程;
(2)设垂直于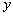 轴的直线
轴的直线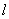 交椭圆于
交椭圆于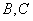 两点, 试求
两点, 试求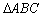 面积的最大值;
面积的最大值;
(3)过点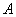 作两条斜率分别为
作两条斜率分别为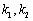 的直线交椭圆于
的直线交椭圆于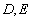 两点,且
两点,且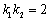 , 求证: 直线
, 求证: 直线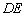 恒过一个定点.
恒过一个定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com