
【题目】已知函数![]() 与
与![]() 的图像相交于点
的图像相交于点![]() ,
,![]() 两点,若动点
两点,若动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹方程是______.
的轨迹方程是______.
【答案】(x﹣1)2+(y﹣1)2=4.
【解析】
函数f(x)![]() 1
1![]() ,可得f(x)的对称中心为Q(1,1).直线g(x)=mx+1﹣m即y=m(x﹣1)+1,经过定点Q(1,1).可得两图象相交的两点A,B关于点Q对称.设A(x0,y0),B(2﹣x0,2﹣y0).设P(x,y).利用动点P满足|
,可得f(x)的对称中心为Q(1,1).直线g(x)=mx+1﹣m即y=m(x﹣1)+1,经过定点Q(1,1).可得两图象相交的两点A,B关于点Q对称.设A(x0,y0),B(2﹣x0,2﹣y0).设P(x,y).利用动点P满足|![]() |=4,即可得出.
|=4,即可得出.
函数f(x)![]() 1
1![]() ,可得f(x)的对称中心为Q(1,1).
,可得f(x)的对称中心为Q(1,1).
直线g(x)=mx+1﹣m即y=m(x﹣1)+1,经过定点Q(1,1).
则两图象相交的两点A,B关于点Q对称.
设A(x0,y0),B(2﹣x0,2﹣y0).设P(x,y).
∵![]() (2﹣2x,2﹣2y).
(2﹣2x,2﹣2y).
∵动点P满足|![]() |=4,∴
|=4,∴![]() 4,
4,
化为:(x﹣1)2+(y﹣1)2=4.
故答案为:(x﹣1)2+(y﹣1)2=4.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】如图,直角梯形ABDC中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
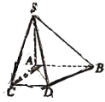
(1)若S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线,并说明理由;
(2)直角梯形ABDC绕直线AC所在直线旋转一周所得几何体名称是什么?并求出其体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市政府为了节约用水,调查了100位居民某年的月均用水量(单位:![]() ),频数分布如下:
),频数分布如下:
分组 |
|
|
|
|
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根据所给数据将频率分布直图补充完整(不必说明理由);
(2)根据频率分布直方图估计本市居民月均用水量的中位数;
(3)根据频率分布直方图估计本市居民月均用水量的平均数(同一组数据由该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解人们对“延迟退休年龄政策”的态度,某部门从网年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:

(I)由频率分布直方图估计年龄的众数和平均数;
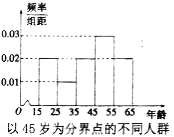
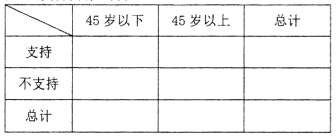
(II)由以上统计数据填2×2列联表,并判断是否有95%的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
参考数据:
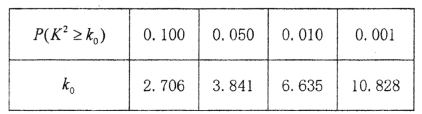
![]()
(III)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人.求抽到的2人中1人是45岁以下,另一人是45岁以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() ,
,![]() ,给出下列曲线方程:(1)
,给出下列曲线方程:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,在曲线上存在点
,在曲线上存在点![]() 满足
满足![]() 的所有曲线是( )
的所有曲线是( )
A.(1)(2)(3)(4)B.(2)(3)
C.(1)(4)D.(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数![]() 与复平面上点
与复平面上点![]() 对应.
对应.
(1)若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的一个虚根,且
的一个虚根,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)设复数![]() 满足条件
满足条件![]() (其中
(其中![]() 、常数
、常数![]() ),当
),当![]() 为奇数时,动点
为奇数时,动点![]() 的轨迹为
的轨迹为![]() ,当
,当![]() 为偶数时,动点
为偶数时,动点![]() 的轨迹为
的轨迹为![]() ,且两条曲线都经过点
,且两条曲线都经过点![]() ,求轨迹
,求轨迹![]() 与
与![]() 的方程;
的方程;
(3)在(2)的条件下,轨迹![]() 上存在点
上存在点![]() ,使点
,使点![]() 与点
与点![]() 的最小距离不小于
的最小距离不小于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+my+1=0和l2:(m-3)x-2y+(13-7m)=0.
(1)若l1⊥l2,求实数m的值;
(2)若l1∥l2,求l1与l2之间的距离d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是函数
是函数![]() 的图象上任意两点,若
的图象上任意两点,若![]() 为
为![]() ,
,![]() 的中点,且
的中点,且![]() 的横坐标为
的横坐标为![]() .
.
(1)求![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)已知数列![]() 的通项公式
的通项公式![]() (
(![]() ,
,![]() ),数列
),数列![]() 的前
的前![]() 项和为
项和为![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com