
分析 (I)将函数进行化简,结合三角函数的图象和性质和已知坐标,即可求函数ω和φ的值;
(II)求出函数y=f(2x)的解析式,根据x∈[0,$\frac{π}{2}$]求出函数y=f(2x)的范围,在求其范围内的最大值和最小值,即可得到值域.
解答 解:f(x)=$\frac{1}{2}$sin2ωxcosφ+cos2ωxsinφ+$\frac{1}{2}$cos($\frac{π}{2}$+φ)(0<φ<π),
?f(x)=$\frac{1}{2}$sin2ωxcosφ+cos2ωxsinφ-$\frac{1}{2}$sinφ
?f(x)=$\frac{1}{2}$sin2ωxcosφ+sinφ(cos2ωx-$\frac{1}{2}$)
?f(x)=$\frac{1}{2}$sin2ωxcosφ+$\frac{1}{2}$cos2ωxsinφ
?f(x)=$\frac{1}{2}$sin(2ωx+φ),
(I)∵图象上相邻两条对称轴之间的距离为π,∴T=2π,
又∵T=$\frac{2π}{|2ω|}$,∴ω=$±\frac{1}{2}$,
图象过点($\frac{π}{6},\frac{1}{2}$),∴$\frac{1}{2}$=$\frac{1}{2}$sin(±1×$\frac{π}{6}$+φ),
解得:$φ=\frac{π}{3}或φ=\frac{2π}{3}$,
∴f(x)=$\frac{1}{2}$sin(x+$\frac{π}{3}$)或f(x)=$\frac{1}{2}$sin(-x+$\frac{2π}{3}$);
(Ⅱ)∵y=f(2x),
∴y=f(2x)=$\frac{1}{2}$sin(2x+$\frac{π}{3}$),【注意:只需要一个解析式即可,其实两个解析式化简是一样的】
又∵x∈[0,$\frac{π}{2}$],
∴2x+$\frac{π}{3}$∈[$\frac{π}{3},\frac{4π}{3}$],
结合正弦函数的图象和性质:当$x=\frac{π}{2}$时,y取得最大值,即${y}_{max}=\frac{1}{2}sin\frac{π}{2}=\frac{1}{2}$,
当$x=\frac{4π}{3}$时,y取得最小值,即${y}_{min}=\frac{1}{2}sin\frac{4π}{3}=\frac{1}{2}×(-\frac{\sqrt{3}}{2})=-\frac{\sqrt{3}}{4}$,
所以函数y=f(2x),x∈[0,$\frac{π}{2}$]的值域为$[-\frac{\sqrt{3}}{4},\frac{1}{2}]$.
点评 本题主要考查三角函数的图象和性质,三角函数的化简能力和计算能力,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
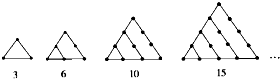 把3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第六个三角形数是( )
把3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第六个三角形数是( )| A. | 27 | B. | 28 | C. | 29 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
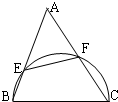 如图,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE.
如图,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理 成绩好 | 物理 成绩不好 | 合计 | |
| 数学 成绩好 | 62 | 23 | 85 |
| 数学 成绩不好 | 28 | 22 | 50 |
| 合计 | 90 | 45 | 135 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com