
分析 (1)当a=-4时,先求导,根据导数大于0,解不等式求出f(x)的单调递增区间;
(2)利用导数判断函数的单调性,从而得出函数在闭区间上的最小值,即得到参数的一个方程,从而求出参数的值;
(3)求出导数,令导数不大于0,可得减区间,再由题意可得有-$\frac{a}{10}$≤1<4≤-$\frac{a}{2}$,解不等式即可得到所求范围.
解答 解;(1)当a=-4时,f(x)=(4x2-16x+16)$\sqrt{x}$,
∴f′(x)=(8x-16)$\sqrt{x}$+(4x2-16x+16)$\frac{1}{2\sqrt{x}}$
=2$\sqrt{x}$(5x+$\frac{4}{x}$-12)=$\frac{2\sqrt{x}}{x}$(5x2-12x+4),
∵f′(x)>0,x≥0,
∴5x2-12x+4>0
解得,x>2或0<x<$\frac{2}{5}$,
∴f(x)的单调递增区间为(0,$\frac{2}{5}$),(2,+∞);
(2)∵f(x)=(4x2+4ax+a2)$\sqrt{x}$,
∴f′(x)=$\frac{\sqrt{x}}{2x}$(20x2+12ax+a2),
令f′(x)=0.解得x=$\frac{-a}{10}$或$\frac{-a}{2}$,
当f′(x)>0时,x在(0,$\frac{-a}{10}$),($\frac{-a}{2}$,+∞)为单调递增,
当f′(x)<0时,x在($\frac{-a}{10}$,$\frac{-a}{2}$)上单调递减,
①当$\frac{-a}{10}$≥4,即a≤-40,f(x)在区间[1,4]为增函数,
由f(1)=8,解得a=-2±2$\sqrt{2}$,不符合舍去.
②当$\frac{-a}{2}$≤1,即-2≤a<0时,f(x)在区间[1,4]为增函数,
由f(1)=8,解得a=-2±2$\sqrt{2}$,不符合舍去.
③当$\frac{-a}{10}$≤1,且$\frac{-a}{2}$≥4,即-10≤a≤-8时,f(x)在区间[1,4]为减函数,
由f(4)=8,解得a=-10;
④当1<$\frac{-a}{10}$<4,即-40<a<-10时,由f(1)=8或f(4)=8,
解得,a=-2±2$\sqrt{2}$,或a=-6,a=-10,不符合舍去,
⑤当1<$\frac{-a}{2}$<4,即-8<a<-4时,由f(-$\frac{a}{2}$)=8,无解.
综上所述,a=-10;
(3)由f(x)的导数为f′(x)=$\frac{\sqrt{x}}{2x}$(20x2+12ax+a2),
令f′(x)≤0,可得-$\frac{a}{10}$≤x≤-$\frac{a}{2}$,
由题意可得[1,4]⊆[-$\frac{a}{10}$,-$\frac{a}{2}$],
即有-$\frac{a}{10}$≤1<4≤-$\frac{a}{2}$,
解得-10≤a≤-8.
点评 本题考查的是导数知识,重点是利用导数判断函数的单调性,难点是分类讨论.对学生的能力要求较高,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 如果a>b,c≠0,那么$\frac{a}{c}>\frac{b}{c}$ | B. | 如果a>b,那么a2>b2 | ||
| C. | 如果a>b,c>d,那么a+d>b+c | D. | 如果a>b,c>d,那么a-d>b-c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|x≥-2} | C. | {x|0≤x≤1} | D. | {x|-4≤x≤0且x≠-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
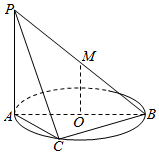 如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:
如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com