
【题目】在四棱锥![]() 中,
中,![]() 为
为![]() 与
与![]() 的交点,
的交点,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() ,
,![]() .
.
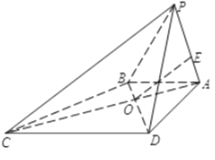
(1)求异面直线![]() 和
和![]() 所成角的大小;
所成角的大小;
(2)若点![]() 为棱
为棱![]() 上一点,且
上一点,且![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)求证:平面![]() 平面
平面![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)由![]() 可得异面直线
可得异面直线![]() 和
和![]() 所成角为
所成角为![]() 和
和![]() 所成角,进而求解即可;
所成角,进而求解即可;
(2)由![]() 平面
平面![]() 可得
可得![]() ,则
,则![]() ,再由
,再由![]() 求解即可;
求解即可;
(3)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,由正三角形可得
,由正三角形可得![]() ,再利用勾股定理可得
,再利用勾股定理可得![]() ,进而求证即可.
,进而求证即可.
(1)因为![]() ,所以异面直线
,所以异面直线![]() 和
和![]() 所成角为
所成角为![]() 和
和![]() 所成角,即
所成角,即![]() ,
,
因为![]() 是正三角形,
是正三角形,![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 是等腰直角三角形,
是等腰直角三角形,
所以![]() ,
,
即异面直线![]() 和
和![]() 所成角为
所成角为![]()
(2)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]()
(3)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() 是正三角形,
是正三角形,![]() ,所以
,所以![]() ,
,
因为![]() 是
是![]() 中点,所以
中点,所以![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
设![]() ,在等腰直角三角形
,在等腰直角三角形![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
在直角梯形![]() 中,
中,![]() ,
,
因为![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,由
中,由![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,
,
所以![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()


科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
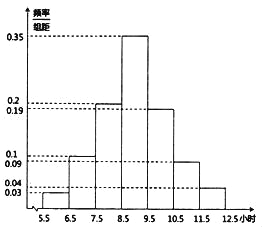
(1)求这200名学生每周阅读时间的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .利用直方图得到的正态分布,求
.利用直方图得到的正态分布,求![]() .
.
(ii)从该高校的学生中随机抽取20名,记![]() 表示这20名学生中每周阅读时间超过10小时的人数,求
表示这20名学生中每周阅读时间超过10小时的人数,求![]() (结果精确到0.0001)以及
(结果精确到0.0001)以及![]() 的数学期望.
的数学期望.
参考数据:![]() ,
,![]() .若
.若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形无底仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12m,高4m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆C:![]() (a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=
(a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=![]() 与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com