
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 求出数列{bn}的通项,利用叠加法求出数列{an}的通项,进而求和,即可求极限.
解答 解:由题意,{bn}是首项为1,公比为2的等比数列,
∴bn=2n-1.
∵bn=an-an-1,
∴an=(b2+b3+…+bn)+a1=$\frac{1-{2}^{n}}{1-2}$=2n-1,
∴Sn=a1+a2+…+an=$\frac{2(1-{2}^{n})}{1-2}$-n=2n+1-n-2,
∴$\underset{lim}{n→∞}$$\frac{{S}_{n}}{{a}_{n}}$=$\underset{lim}{n→∞}$$\frac{{2}^{n+1}-n-2}{{2}^{n}-1}$=$\underset{lim}{n→∞}$$\frac{2-\frac{n}{{2}^{n}}-\frac{2}{{2}^{n}}}{1-\frac{1}{{2}^{n}}}$=2,
故选:C.
点评 本题考查等比数列的通项与求和,考查极限的计算,考查学生分析解决问题的能力,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
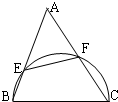 如图,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE.
如图,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=-1,n=1 | B. | m=1,n=1 | C. | m=1,n=-1 | D. | m=-1,n=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com