
分析 (1)由已知中f(-1)=$\frac{5}{2}$,f(0)=2,构造方程求出a,b的值,进而根据奇偶性的定义,可得结论;
(2)证法一:设x1,x2是区间(0,+∞)上的两个任意实数,且x1<x2,作差判断f(x1),f(x2)的大小,可得结论;
证法二:求导,根据x∈(0,+∞)时,f′(x)>0恒成立,可得:函数f(x)在(0,+∞)上为单调递增函数;
(3)若关于x的方程mf(x)=2-x在[-1,1]上有解,即m=$\frac{{2}^{-x}}{{2}^{x}+{2}^{-x}}$在[-1,1]上有解,求出f(x)=$\frac{{2}^{-x}}{{2}^{x}+{2}^{-x}}$的值域,可得答案.
解答 解:(1)∵f(-1)=$\frac{5}{2}$,f(0)=2.
∴$\frac{1}{2}$+2-a+b=$\frac{5}{2}$,1+2b=2,
解得:a=-1,b=0,
∴f(x)=2x+2-x;
函数的定义域为R,
且f(-x)=2-x+2x=f(x),
故函数为偶函数,
(2)证法一:设x1,x2是区间(0,+∞)上的两个任意实数,且x1<x2,
于是f(x2)-f(x1)=(${2}^{{x}_{1}}+{2}^{-{x}_{1}}$)-(${2}^{{x}_{2}}+{2}^{-{x}_{2}}$)=(${2}^{{x}_{1}}-{2}^{{x}_{2}}$)$\frac{{2}^{{x}_{1}}•{2}^{{x}_{2}}-1}{{2}^{{x}_{1}}•{2}^{{x}_{2}}}$.
因为x2>x1>0,所以${2}^{{x}_{1}}>1$,${2}^{{x}_{2}}>1$,${2}^{{x}_{1}}-{2}^{{x}_{2}}<0$,
所以f(x2)-f(x1)>0,所以f(x1)<f(x2),
所以函数f(x)在(0,+∞)上为单调增函数.
证法二:∵f(x)=2x+2-x.
∴f′(x)=ln2•(2x+2-x).
当x∈(0,+∞)时,
f′(x)>0恒成立,
故函数f(x)在(0,+∞)上为单调递增函数;
(3)若关于x的方程mf(x)=2-x在[-1,1]上有解,
即m=$\frac{{2}^{-x}}{{2}^{x}+{2}^{-x}}$在[-1,1]上有解,
令f(x)=$\frac{{2}^{-x}}{{2}^{x}+{2}^{-x}}$=$\frac{1}{{2}^{2x}+1}$,
则f(x)∈[$\frac{1}{5}$,$\frac{4}{5}$],
故m∈[$\frac{1}{5}$,$\frac{4}{5}$].
点评 本题考查的知识点是函数单调性的证明与应用,利用导数研究函数的单调性,难度中档.


科目:高中数学 来源: 题型:解答题
 甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:
甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
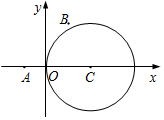 如图,在平面直角坐标系xOy中,已知圆C:x2+y2-4x=0及点A(-1,0),B(1,2)
如图,在平面直角坐标系xOy中,已知圆C:x2+y2-4x=0及点A(-1,0),B(1,2)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com