
 甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:
甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:分析 (1)根据茎叶图中的数据计算甲的中位数乙的众数即可;
(2)计算甲、乙的平均数与方差,比较即可得出结论.
解答 解:(1)将甲的命中个数从小到大排列为5,8,9,11,16,17,
所以甲的中位数是$\frac{9+11}{2}=10$,
将乙的命中个数从小到大排列为6,9,10,12,12,17,
所以乙的众数为12;
(2)甲命中个数的平均数为:
$\overline{X_甲}=\frac{5+8+9+11+16+17}{6}=11$,
乙命中个数的平均数为:
$\overline{X_乙}=\frac{6+9+10+12+12+17}{6}=11$,
甲的方差为:
${S_甲}^2=\frac{1}{6}[{{{(5-11)}^2}+{{(8-11)}^2}+{{(9-11)}^2}+{{(11-11)}^2}+{{(16-11)}^2}+{{(17-11)}^2}}]=\frac{55}{3}$,
乙的方差为:
${S_乙}^2=\frac{1}{6}[{{{(6-11)}^2}+{{(9-11)}^2}+{{(10-11)}^2}+{{(12-11)}^2}+{{(12-11)}^2}+{{(17-11)}^2}}]=\frac{34}{3}$,
因为$\overline{X_甲}=\overline{X_乙}$,${S_甲}^2>{S_乙}^2$,
所以甲乙两人的罚球水平相当,但乙比甲稳定.
点评 本题考查了利用茎叶图中的数据计算中位数、众数以及平均数与方差的应用问题,是基础题目.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-1,2) | C. | (1,2) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
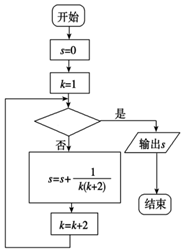
| A. | k>8? | B. | k≥9? | C. | k≥10? | D. | k>11? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (0,2) | C. | (0,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com