
分析 (1)利用二倍角公式以及两角和与差的三角函数化简,然后通过正弦函数的单调增区间求解即可.
(2)求出相位的范围,利用正弦函数的有界性,求解函数的值域即可.
解答 解:(1)$f(x)={sin^2}x+\sqrt{3}sinxcosx=\frac{1-cos2x}{2}+\frac{{\sqrt{3}}}{2}sin2x=sin(2x-\frac{π}{6})+\frac{1}{2}$…(2分)
令$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$解得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}$…(5分)
f(x)的递增区间为$[{kπ-\frac{π}{6},kπ+\frac{π}{3}}](k∈Z)$…(6分)
(2)∵$0≤x≤\frac{π}{2}$,∴$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{5π}{6}$…(8分)
∴$-\frac{1}{2}≤sin(2x-\frac{π}{6})≤1$,∴$0≤sin(2x-\frac{π}{6})+\frac{1}{2}≤\frac{3}{2}$…(10分)
∴f(x)的值域是$[{0,\frac{3}{2}}]$…(12分)
点评 本题考查两角和与差的三角函数,二倍角公式的应用,三角函数的最值,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | λ>-1 | B. | λ<-1 | C. | λ>-$\frac{3}{2}$ | D. | λ<-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:
甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
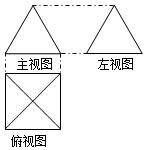 如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位:cm),则此几何体的表面积是( )
如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位:cm),则此几何体的表面积是( )| A. | 8cm2 | B. | $4\sqrt{3}$ cm2 | C. | 12 cm2 | D. | $4+4\sqrt{3}$ cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5-12i | B. | -5+12i | C. | 5-12i | D. | 5+12i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
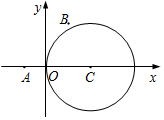 如图,在平面直角坐标系xOy中,已知圆C:x2+y2-4x=0及点A(-1,0),B(1,2)
如图,在平面直角坐标系xOy中,已知圆C:x2+y2-4x=0及点A(-1,0),B(1,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com