
| A. | (2,+∞) | B. | (0,2) | C. | (0,4) | D. | (4,+∞) |
分析 构造已知条件,f(x)-$\frac{8}{x}$>0可得$\frac{8-xf(x)}{x}<0$,f(2)=4,则2f(2)=8,带入即可得到答案.
解答 解:定义在(0,+∞)上的函数f(x)满足:$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0.
∵f(2)=4,则2f(2)=8,
f(x)-$\frac{8}{x}$>0化简得$\frac{8-xf(x)}{x}<0$,
当x<2时,
$\frac{8-xf(x)}{x}<0$⇒$\frac{2f(2)-xf(x)}{2-x}<0$成立.
故得x<2,
∵定义在(0,+∞)上.
∴不等式f(x)-$\frac{8}{x}$>0的解集为(0,2).
故选B.
点评 本题考查了构造已知条件求解不等式,从已知条件入手,找个关系求解.属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1365石 | B. | 338石 | C. | 168石 | D. | 134石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:
甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x2 | C. | y=-x|x| | D. | y=x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
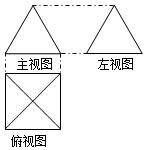 如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位:cm),则此几何体的表面积是( )
如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位:cm),则此几何体的表面积是( )| A. | 8cm2 | B. | $4\sqrt{3}$ cm2 | C. | 12 cm2 | D. | $4+4\sqrt{3}$ cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com