
【题目】在一次抽样调查中测得样本的5个样本点,数值如下表:
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
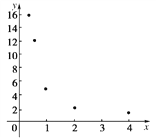
(1)根据散点图判断,![]() 哪一个适宜作为
哪一个适宜作为![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果试建立![]() 与
与![]() 之间的回归方程.(注意
之间的回归方程.(注意![]() 或
或![]() 计算结果保留整数)
计算结果保留整数)
(3)由(2)中所得设z=![]() +
+![]() 且
且![]() ,试求z的最小值。
,试求z的最小值。
参考数据及公式如下:
![]() ,
,![]() ,
,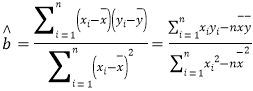
科目:高中数学 来源: 题型:
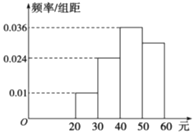
【题目】某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在![]() 元的学生有60人,则下列说法正确的是______.
元的学生有60人,则下列说法正确的是______.
A.样本中支出在![]() 元的频率为
元的频率为![]()
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2000名学生,则定有600人支出在![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将现有![]() 名男生和
名男生和![]() 名女生站成一排照相.(用数字作答)
名女生站成一排照相.(用数字作答)
(1)两女生相邻,有多少种不同的站法?
(2)两名女生不相邻,有多少种不同的站法?
(3)女生甲不在左端,女生乙不在右端,有多少种不同的站法?
(4)女生甲要在女生乙的右方(可以不相邻)有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2asinωxcosωx+2 ![]() cos2ωx﹣
cos2ωx﹣ ![]() (a>0,ω>0)的最大值为2,且最小正周期为π. (I)求函数f(x)的解析式及其对称轴方程;
(a>0,ω>0)的最大值为2,且最小正周期为π. (I)求函数f(x)的解析式及其对称轴方程;
(II)若f(α)= ![]() ,求sin(4α+
,求sin(4α+ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com