
分析 (Ⅰ)根据题意,由正弦定理可得sinC=$\sqrt{3}$sinBsinC-sinCcosB,进而变形可得1=$\sqrt{3}$sinC-cosB,由正弦的和差公式可得1=2sin(B-$\frac{π}{6}$),即可得B-$\frac{π}{6}$的值,计算可得B的值,即可得答案;
(Ⅱ)由余弦定理可得(a+c)2-3ac=12,又由a、b、c成等比数列,进而可以变形为12=(a+c)2-36,解可得a+c=4$\sqrt{3}$,进而计算可得△ABC的周长l=a+b+c,由面积公式S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$b2sinB计算可得△ABC的面积.
解答 解:(Ⅰ)根据题意,若c=$\sqrt{3}$bsinC-ccosB,
由正弦定理可得sinC=$\sqrt{3}$sinBsinC-sinCcosB,
又由sinC≠0,则有1=$\sqrt{3}$sinC-cosB,
即1=2sin(B-$\frac{π}{6}$),
则有B-$\frac{π}{6}$=$\frac{π}{6}$或B-$\frac{π}{6}$=$\frac{5π}{6}$,即B=$\frac{π}{3}$或π(舍)
故B=$\frac{π}{3}$;
(Ⅱ)已知b=2$\sqrt{3}$,则b2=a2+c2-2accosB=a2+c2-ac=(a+c)2-3ac=12,
又由a、b、c成等比数列,即b2=ac,
则有12=(a+c)2-36,解可得a+c=4$\sqrt{3}$,
所以△ABC的周长l=a+b+c=2$\sqrt{3}$+4$\sqrt{3}$=6$\sqrt{3}$,
面积S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$b2sinB=3$\sqrt{3}$.
点评 本题考查正弦、余弦定理的应用,关键利用三角函数的恒等变形正确求出B的值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
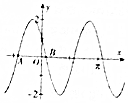 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | B. | [$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{6}$+2kπ,$\frac{π}{3}$+2kπ](k∈Z) | D. | [$\frac{π}{3}$+2kπ,$\frac{5π}{6}$+2kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 4 | 5 | 6 |
| 销售轿车y(台数) | 3 | 4 | 6 | 10 | 12 |
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.
如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1-ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
| 销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com