
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F为棱AD、AB的中点. 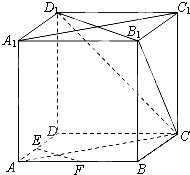
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1 .
【答案】
(1)证明:连接BD.
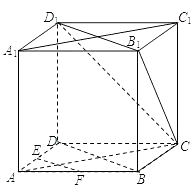
在正方体AC1中,对角线BD∥B1D1.
又因为E、F为棱AD、AB的中点,
所以EF∥BD.
所以EF∥B1D1.
又B1D1平面CB1D1,EF平面CB1D1,
所以EF∥平面CB1D1.
(2)证明:因为在正方体AC1中,
AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
所以AA1⊥B1D1.
又因为在正方形A1B1C1D1中,A1C1⊥B1D1,
所以B1D1⊥平面CAA1C1.
又因为B1D1平面CB1D1,
所以平面CAA1C1⊥平面CB1D1.
【解析】(1)欲证EF∥平面CB1D1 , 根据直线与平面平行的判定定理可知只需证EF与平面CB1D1内一直线平行,连接BD,根据中位线可知EF∥BD,则EF∥B1D1 , 又B1D1平面CB1D1 , EF平面CB1D1 , 满足定理所需条件;(2)欲证平面CAA1C1⊥平面CB1D1 , 根据面面垂直的判定定理可知在平面CB1D1内一直线与平面CAA1C1垂直,而AA1⊥平面A1B1C1D1 , B1D1平面A1B1C1D1 , 则AA1⊥B1D1 , A1C1⊥B1D1 , 满足线面垂直的判定定理则B1D1⊥平面CAA1C1 , 而B1D1平面CB1D1 , 满足定理所需条件.
【考点精析】关于本题考查的直线与平面平行的判定和平面与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,设
,设![]() :当
:当![]() 时,不等式
时,不等式![]() 恒成立;Q:当
恒成立;Q:当![]() 时,
时,![]() 是单调函数。如果满足
是单调函数。如果满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,满足Q成立的
,满足Q成立的![]() 的集合记为
的集合记为![]() ,求A∩(CRB)(
,求A∩(CRB)(![]() 为全集).
为全集).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.35
B.﹣3
C.3
D.﹣0.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B分别是直线y=x和y=﹣x上的两个动点,线段AB的长为2 ![]() ,D是AB的中点.
,D是AB的中点.
(1)求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,
①当|PQ|=3时,求直线l的方程;
②试问在x轴上是否存在点E(m,0),使 ![]()
![]() 恒为定值?若存在,求出E点的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E点的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
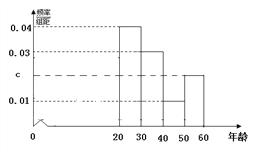
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【广西名校2017届高三上学期第一次摸底】如图,过抛物线![]() 上一点
上一点![]() ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于![]() ,
,![]() ,
,
当![]() 与
与![]() 的斜率存在且倾斜角互补时:
的斜率存在且倾斜角互补时:
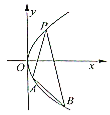
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 时,求
时,求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过
两点,过![]() 与
与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com