
【题目】在锐角△ABC中,角A,B,C的对边分别为a,b,c,满足 ![]() =
= ![]() .
.
(1)求角A的大小;
(2)若a= ![]() ,△ABC的面积S△ABC=3
,△ABC的面积S△ABC=3 ![]() ,求b+c的值,;
,求b+c的值,;
(3)若函数f(x)=2sinxcos(x+ ![]() ),求f(B)的取值范围.
),求f(B)的取值范围.
【答案】
(1)解:锐角△ABC中,角A,B,C的对边分别为a,b,c,满足 ![]() =
= ![]() ,
,
∴ ![]() =
= 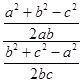 ,
,
整理,得bc=b2+c2﹣a2,
∴cosA= ![]() =
= ![]() =
= ![]() ,
,
∴A= ![]() .
.
(2)解:∵a= ![]() ,△ABC的面积S△ABC=3
,△ABC的面积S△ABC=3 ![]() ,A=
,A= ![]() ,
,
∴S△ABC= ![]() =3
=3 ![]() ,解得bc=12,
,解得bc=12,
cosA= ![]() =
= ![]() =
= ![]() ,解得b2+c2=25,
,解得b2+c2=25,
∴(b+c)2=b2+c2+2bc=25+24=49,
∴b+c=7
(3)解:∵f(x)=2sinxcos(x+ ![]() )
)
=2sinx(cosxcos ![]() ﹣sinxsin
﹣sinxsin ![]() )
)
= ![]() sinxcosx﹣sin2x
sinxcosx﹣sin2x
= ![]() sin2x﹣
sin2x﹣ ![]()
= ![]() sin2x+
sin2x+ ![]() cos2x﹣
cos2x﹣ ![]()
=cos ![]() sin2x+sin
sin2x+sin ![]() cos2x﹣
cos2x﹣ ![]()
=sin(2x+ ![]() )﹣
)﹣ ![]() ,
,
∵A= ![]() ,∴锐角△ABC中,B∈(0,
,∴锐角△ABC中,B∈(0, ![]() ),∴2B+
),∴2B+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
f(B)=sin(2B+ ![]() )﹣
)﹣ ![]() ,
,
当2B+ ![]() =
= ![]() 时,f(B)max=1﹣
时,f(B)max=1﹣ ![]() =
= ![]() ,
,
当2B+ ![]() =
= ![]() 时,f(B)min=﹣
时,f(B)min=﹣ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ﹣
﹣ ![]() .
.
∴f(B)的取值范围是(﹣ ![]() ,
, ![]() )
)
【解析】(1)利用余弦定理推导出bc=b2+c2﹣a2,从而求出cosA= ![]() ,进而能求出A.(2)由S△ABC=
,进而能求出A.(2)由S△ABC= ![]() =3
=3 ![]() ,得bc=12,由余弦定理求出b2+c2=25,从而求出(b+c)2,进而求出b+c的值.(3)由f(x)=2sinxcos(x+
,得bc=12,由余弦定理求出b2+c2=25,从而求出(b+c)2,进而求出b+c的值.(3)由f(x)=2sinxcos(x+ ![]() )=sin(2x+
)=sin(2x+ ![]() )﹣
)﹣ ![]() ,A=
,A= ![]() ,得2B+
,得2B+ ![]() ∈(
∈( ![]() ,
, ![]() ),由此能求出f(B)=sin(2B+
),由此能求出f(B)=sin(2B+ ![]() )﹣
)﹣ ![]() 的取值范围.
的取值范围.


科目:高中数学 来源: 题型:
【题目】某校在高二年级开设选修课,其中数学选修课开了三个班.选课结束后,有四名选修英语的同学要求改修数学,但数学选修每班至多可再接收两名同学,那么安排好这四名同学的方案有( )
A.72种
B.54种
C.36种
D.18种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2x2+bx+c,不等式f(x)<0的解集为(0,5).
(1)求b,c的值;
(2)若对任意x∈[﹣1,1],不等式f(x)+t≤2恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C的对边长分别为a,b,c,R是△ABC的外接圆半径,有下列四个条件: ⑴(a+b+c)(a+b﹣c)=3ab
⑵sinA=2cosBsinC
⑶b=acosC,c=acosB
⑷ ![]()
有两个结论:甲:△ABC是等边三角形.乙:△ABC是等腰直角三角形.
请你选取给定的四个条件中的两个为条件,两个结论中的一个为结论,写出一个你认为正确的命题 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1+2a2++22a3+…2n﹣1an=(n2n﹣2n+1)t对任意n∈N*成立,其中常数t>0.若关于n的不等式 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 的解集为{n|n≥4,n∈N*},则实数m的取值范围是 .
的解集为{n|n≥4,n∈N*},则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P是圆O:x2+y2=1与x轴正半轴的交点,半径OA在x轴的上方,现将半径OA绕原点O逆时针旋转 ![]() 得到半径OB.设∠POA=x(0<x<π),
得到半径OB.设∠POA=x(0<x<π), ![]() .
. 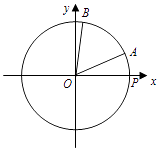
(1)若 ![]() ,求点B的坐标;
,求点B的坐标;
(2)求函数f(x)的最小值,并求此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x﹣2y+3=0和l2:x+2y﹣9=0的交点为A.
(1)求过点A,且与直线2x+3y﹣1=0平行的直线方程;
(2)求过点A,且倾斜角为直线l1倾斜角2倍的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ. 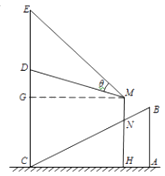
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com