
【题目】△ABC的三个内角A,B,C的对边长分别为a,b,c,R是△ABC的外接圆半径,有下列四个条件: ⑴(a+b+c)(a+b﹣c)=3ab
⑵sinA=2cosBsinC
⑶b=acosC,c=acosB
⑷ ![]()
有两个结论:甲:△ABC是等边三角形.乙:△ABC是等腰直角三角形.
请你选取给定的四个条件中的两个为条件,两个结论中的一个为结论,写出一个你认为正确的命题 .
【答案】(1)(2)→甲 或 (2)(4)→乙 或 (3)(4)→乙
【解析】解:由(1)(2)为条件,甲为结论,得到的命题为真命题,理由如下:
证明:由(a+b+c)(a+b﹣c)=3ab,变形得:
a2+b2+2ab﹣c2=3ab,即a2+b2﹣c2=ab,
则cosC= ![]() =
= ![]() ,又C为三角形的内角,
,又C为三角形的内角,
∴C=60°,
又sinA=sin(B+C)=sinBcosC+cosBsinC=2cosBsinC,
即sinBcosC﹣cosBsinC=sin(B﹣C)=0,
∵﹣π<B﹣C<π,
∴B﹣C=0,即B=C,
则A=B=C=60°,
∴△ABC是等边三角形;
以(2)(4)作为条件,乙为结论,得到的命题为真命题,理由为:
证明:化简得:sinA=sin(B+C)=sinBcosC+cosBsinC=2cosBsinC,
即sinBcosC﹣cosBsinC=sin(B﹣C)=0,
∵﹣π<B﹣C<π,
∴B﹣C=0,即B=C,
∴b=c,
由正弦定理 ![]() =
= ![]() =
= ![]() =2R得:
=2R得:
sinA= ![]() ,sinB=
,sinB= ![]() ,sinC=
,sinC= ![]() ,
,
代入 ![]() 得:
得:
2R( ![]() ﹣
﹣ ![]() )=(
)=( ![]() a﹣b)
a﹣b) ![]() ,
,
整理得:a2﹣b2= ![]() ab﹣b2,即a2=
ab﹣b2,即a2= ![]() ab,
ab,
∴a= ![]() b,
b,
∴a2=2b2,又b2+c2=2b2,
∴a2=b2+c2,
∴∠A=90°,
则三角形为等腰直角三角形;
以(3)(4)作为条件,乙为结论,得到的命题为真命题,理由为:
证明:由正弦定理 ![]() =
= ![]() =
= ![]() =2R得:
=2R得:
sinA= ![]() ,sinB=
,sinB= ![]() ,sinC=
,sinC= ![]() ,
,
代入 ![]() 得:
得:
2R( ![]() ﹣
﹣ ![]() )=(
)=( ![]() a﹣b)
a﹣b) ![]() ,
,
整理得:a2﹣b2= ![]() ab﹣b2,即a2=
ab﹣b2,即a2= ![]() ab,
ab,
∴a= ![]() b,
b,
∴a2=2b2,又b2+c2=2b2,
∴a2=b2+c2,
∴∠A=90°,
又b=acosC,c=acosB,
根据正弦定理得:sinB=sinAcosC,sinC=sinAcosB,
∴ ![]() =
= ![]() ,即sinBcosB=sinCcosC,
,即sinBcosB=sinCcosC,
∴sin2B=sin2C,又B和C都为三角形的内角,
∴2B=2C,即B=C,
则三角形为等腰直角三角形.
所以答案是:(1)(2)→甲 或 (2)(4)→乙 或 (3)(4)→乙
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点
=1(a>b>0)的左右焦点分别为F1 , F2 , 抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点 ![]() . (I)求椭圆C的标准方程;
. (I)求椭圆C的标准方程;
(Ⅱ)若椭圆C的右顶点为A,直线l交椭圆C于E、F两点(E、F与A点不重合),且满足AE⊥AF,若点P为EF中点,求直线AP斜率的最大值.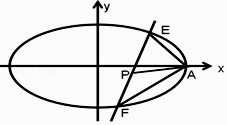
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),函数f(x)=(
),函数f(x)=( ![]() +
+ ![]() )
) ![]() .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈(0, ![]() )时,求函数f(x)的值域.
)时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( ) 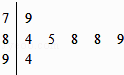
A.86.5,86.7
B.88,86.7
C.88,86.8
D.86,5,86.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an},{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,角A,B,C的对边分别为a,b,c,满足 ![]() =
= ![]() .
.
(1)求角A的大小;
(2)若a= ![]() ,△ABC的面积S△ABC=3
,△ABC的面积S△ABC=3 ![]() ,求b+c的值,;
,求b+c的值,;
(3)若函数f(x)=2sinxcos(x+ ![]() ),求f(B)的取值范围.
),求f(B)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷等差数列{an}的前n项和为Sn , 已知a1=1,S3=12.
(1)求a24与S7的值;
(2)已知m、n均为正整数,满足am=Sn . 试求所有n的值构成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|+2x(a∈R)
(1)当a=4时,解不等式f(x)≥8;
(2)当a∈[0,4]时,求f(x)在区间[3,4]上的最小值;
(3)若存在a∈[0,4],使得关于x的方程f(x)=tf(a)有3个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com