
分析 可求得f(1)=$\frac{5}{4}$sin($\frac{π}{2}$)=$\frac{5}{4}$,作函数的图象,分类讨论即可.
解答 解:f(1)=$\frac{5}{4}$sin($\frac{π}{2}$)=$\frac{5}{4}$,
作函数y=f(x)的图象如右图,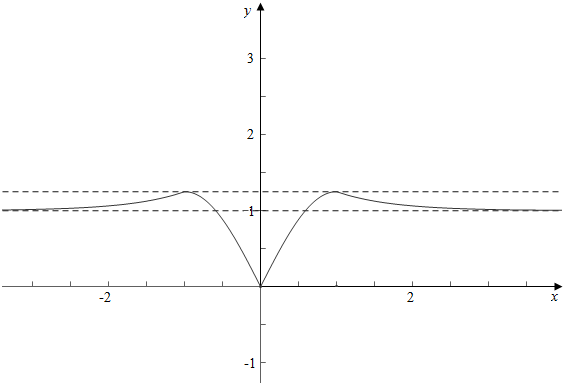
设方程x2+ax+b=0的两个根为x1,x2;
①若x1=$\frac{5}{4}$,1<x2<$\frac{5}{4}$,
故x1+x2=-a∈($\frac{9}{4}$,$\frac{5}{2}$),
故a∈(-$\frac{5}{2}$,-$\frac{9}{4}$);
②若0<x1≤1,1<x2<$\frac{5}{4}$,
故x1+x2=-a∈(1,$\frac{9}{4}$),
故a∈(-$\frac{9}{4}$,-1);
故答案为:$\frac{5}{4}$,(-$\frac{5}{2}$,-$\frac{9}{4}$)∪(-$\frac{9}{4}$,-1).
点评 本题考查了函数的性质的判断与应用,同时考查了数形结合的思想的应用.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
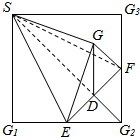 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com