
已知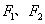 为椭圆
为椭圆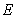 的左右焦点,点
的左右焦点,点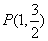 为其上一点,且有
为其上一点,且有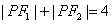
(I)求椭圆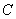 的标准方程;
的标准方程;
(II)过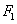 的直线
的直线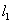 与椭圆
与椭圆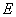 交于
交于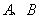 两点,过
两点,过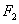 与
与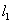 平行的直线
平行的直线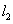 与椭圆
与椭圆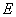 交于
交于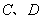 两点,求四边形
两点,求四边形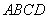 的面积
的面积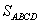 的最大值.
的最大值.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
已知椭圆 的两焦点分别为
的两焦点分别为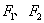 ,
,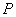 是椭圆在第一象限内的一点,并满足
是椭圆在第一象限内的一点,并满足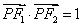 ,过
,过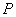 作倾斜角互补的两条直线
作倾斜角互补的两条直线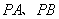 分别交椭圆于
分别交椭圆于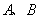 两点. (1)求
两点. (1)求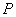 点坐标;(2)当直线
点坐标;(2)当直线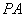 经过点
经过点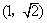 时,求直线
时,求直线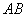 的方程;(3)求证直线
的方程;(3)求证直线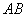 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系中,设点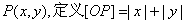 ,其中O为坐标原点,对于以下结论:
,其中O为坐标原点,对于以下结论:
①符合[OP]=1的点P的轨迹围成的图形的面积为2;
②设P为直线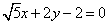 上任意一点,则[OP]的最小值为1;
上任意一点,则[OP]的最小值为1;
③设P为直线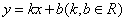 上的任意一点,则“使[OP]最小的点P有无数个”
上的任意一点,则“使[OP]最小的点P有无数个”
的必要不充分条件是“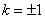 ”.
”.
其中正确的结论有 (填上你认为正确的所有结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
设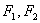 分别为双曲线
分别为双曲线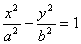
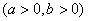 的左、右焦点,
的左、右焦点,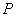 为双曲线右支上任一点。若
为双曲线右支上任一点。若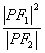 的最小值为
的最小值为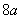 ,则该双曲线的离心率的取值范围是( )
,则该双曲线的离心率的取值范围是( )
A.(1,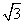 ] B.(1,3) C.(1,3] D.[
] B.(1,3) C.(1,3] D.[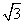 ,3)
,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数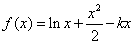 ,其中常数
,其中常数 .
.
(1) 求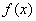 的单调增区间与单调减区间;
的单调增区间与单调减区间;
(2)若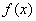 存在极值且有唯一零点
存在极值且有唯一零点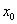 ,求
,求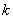 的取值范围及不超过
的取值范围及不超过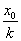 的最大整数
的最大整数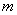 .
.
请考生在第22、23、24三题中任选一题做答,如果多做。则按所做的第一题记分.答题时用2B铅笔在答题卡上把所选的题号涂黑.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com