
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
分析 (1)汽车A在同一周内恰有两天连续出车含两种情况:星期三和星期四出车且星期五不出车和星期四和星期五出车且星期三不出车,由此能求出汽车A在同一周内恰有两天连续出车的概率.
(2)A,B两车同时出车的概率t=pq∈[0.16.0.25],由此能求出两车的日出车频率分别为0.2和0.8时,一周内汽车A,B同日都出车的平均天数最少.
解答 解:(1)汽车A在同一周内恰有两天连续出车含两种情况:
星期三和星期四出车且星期五不出车和星期四和星期五出车且星期三不出车,
∴汽车A在同一周内恰有两天连续出车的概率:
P=0.8×0.8×(1-0.8)+0.8×0.8×(1-0.8)=0.256.
(2)∵p∈[0.4,0.8],且两车的日出车频率之和为1,
∴A,B两车同时出车的概率t=pq∈[0.16.0.25],
∵周六、周日和限行日停止用车,
∴E(ξ)=3pq,其最小值为3×0.16=0.48.
∴两车的日出车频率分别为0.2和0.8时,一周内汽车A,B同日都出车的平均天数最少.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的应用,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.
已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
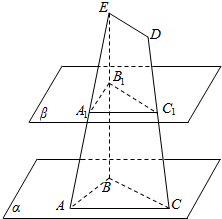 平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.
平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
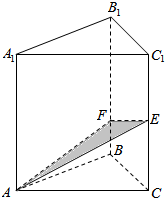 在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.
在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com