
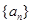 的前
的前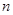 项和为
项和为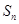 ,
,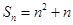 ,数列
,数列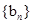 的通项公式为
的通项公式为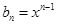 .
.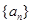 的通项公式;
的通项公式;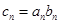 ,数列
,数列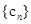 的前
的前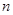 项和为
项和为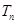 ,
,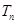 ;
;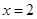 ,求数列
,求数列 的最小项的值.
的最小项的值.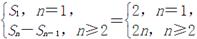 =2n.
=2n.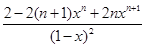 .当x=1时,Tn=n2+n.
.当x=1时,Tn=n2+n.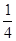 .
.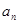 与
与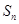 的关系得
的关系得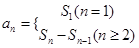 ,又
,又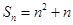 ,
,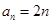 ;(2)由(1)得
;(2)由(1)得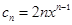 ,讨论
,讨论 分别用公式法和错误相减法求和;
分别用公式法和错误相减法求和;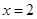 时,
时,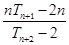 =
=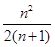 ,构造函数研究单调性得最小值
,构造函数研究单调性得最小值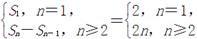 =2n.…………………4分
=2n.…………………4分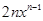 .
.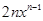 . ①
. ①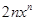 . ②
. ②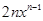 -
-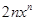 .
. 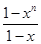 -
-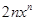 .所以Tn=
.所以Tn=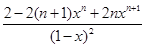 .…8分
.…8分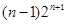 .
.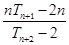 =
=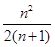 . ……………………11分
. ……………………11分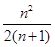 .
. 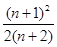 -
-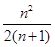 =
=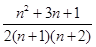 >0, …………14分
>0, …………14分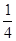 ,即数列{
,即数列{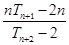 }的最小项的值为
}的最小项的值为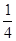


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:不详 题型:解答题
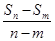 =
=  ;
; +
+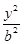 =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com