
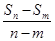 =
=  ;
; +
+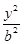 =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之. 的公差为
的公差为
 ,
,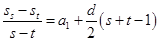 ,
, ,
,
 ;…………3分
;…………3分 的斜率分别为
的斜率分别为 ,则
,则 ,
, ,
, ,
,
 ,即
,即 ;……………………………………6分
;……………………………………6分 图像上有不同的四点
图像上有不同的四点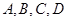 ,若线段
,若线段 的中点连线经过原点,则
的中点连线经过原点,则 .
. ,线段
,线段 的中点不在坐标轴上,且它们的连线经过原点,则
的中点不在坐标轴上,且它们的连线经过原点,则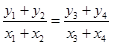 ,
,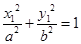 ,
,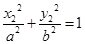 ,
,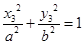 ,
,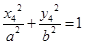
 ,
,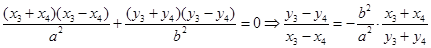 ,
, ,即
,即 ;
; 中点在坐标轴上时,
中点在坐标轴上时, 同时垂直这条坐标轴,
同时垂直这条坐标轴, 成立.
成立. 图像上有不同的四点
图像上有不同的四点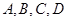 ,设它们的坐标分别是
,设它们的坐标分别是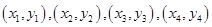 ,若
,若 ,则
,则 .
.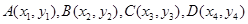 ,又
,又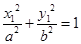 ,
,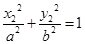 ,
,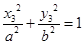 ,
,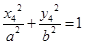

 ,
, ,
, ,即
,即 .
. 时,
时, 同时垂直
同时垂直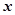 轴,
轴, 成立.
成立. 图像上有四点
图像上有四点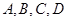 ,设它们的坐标分别是
,设它们的坐标分别是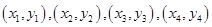 ,若
,若 ,则
,则 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com