练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】《朗读者》是一档文化情感类节目，以个人成长、情感体验、背景故事与传世佳作相结合的方式，选用精美的文字，用最平实的情感读出文字背后的价值，深受人们的喜爱.为了了解人们对该节目的喜爱程度，某调查机构随机调查了，两个城市各100名观众，得到下面的列联表.

    非常喜爱

    喜爱

    合计

    城市

    60

    100

    城市

    30

    合计

    200

    完成上表，并根据以上数据，判断是否有的把握认为观众的喜爱程度与所处的城市有关？

    附参考公式和数据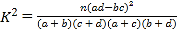：（其中）.

    0.15

    0.10

    0.05

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    【答案】列表见解析，没有的把握认为观众的喜爱程度与所处的城市有关

    【解析】

    由题意填写列联表，根据公式计算观测值，对照临界值得出结论即可.

    完成列联表如下

    非常喜爱

    喜爱

    合计

    城市

    60

    40

    100

    城市

    70

    30

    100

    合计

    130

    70

    200

    的观测值，

    所以没有的把握认为观众的喜爱程度与所处的城市有关.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某同学对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究，他在4月份的天中随机挑选了天进行研究，且分别记录了每天昼夜温差与每天每颗种子浸泡后的发芽数，得到如下数据：

    日期

    4月1日

    4月7日

    4月15日

    4月21日

    4月30日

    昼夜温差/℃

    10

    11

    13

    12

    8

    发芽数/颗

    23

    25

    30

    26

    16

    （1）从这天中任选天，若选取的是4月1日与4月30日的两组数据.请根据这天中的另外天的数据，求出关于的线性回归方程；

    （2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？

    参考公式和数据：线性回归方程，，，，.

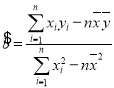    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知x，y满足约束条件，当时，的最小值是________.若的最大值是-1，则________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某服装店对过去100天其实体店和网店的销售量（单位：件）进行了统计，制成频率分布直方图如下：

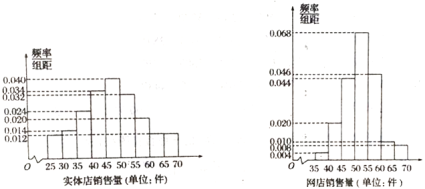
    （1）若将上述频率视为概率，已知该服装店过去100天的销售中，实体店和网店销售量都不低于50件的概率为0.4，求过去100天的销售中，实体店和网店至少有一边销售量不低于50件的天数；

    （2）若将上述频率视为概率，已知该服装店实体店每天的人工成本为500元，门市成本为1200元，每售出一件利润为50元，求该门市一天获利不低于800元的概率；

    （3）根据销售量的频率分布直方图，求该服装店网店销售量中位数的估计值（精确到0.01）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知若椭圆：（）交轴于，两点，点是椭圆上异于，的任意一点，直线，分别交轴于点，，则为定值.

    （1）若将双曲线与椭圆类比，试写出类比得到的命题；

    （2）判定（1）类比得到命题的真假，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在区间[﹣3，5]上随机地取一个数x，若x满足|x|≤m（m＞0）的概率为，则m的值等于

    A. B. 3 C. 4 D. ﹣2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在点处的切线与直线垂直.

    （1）求函数的极值；

    （2）若在上恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且点在函数的图像上；

    （1）求数列的通项公式；

    （2）设数列满足：，，求的通项公式；

    （3）在第（2）问的条件下，若对于任意的，不等式恒成立，求实数的取值范围；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经调查统计，网民在网上光顾某淘宝小店，经过一番浏览后，对该店铺中的三种商品有购买意向．该淘宝小店推出买一种送5元优惠券的活动．已知某网民购买商品的概率分别为，，，至少购买一种的概率为，最多购买两种的概率为．假设该网民是否购买这三种商品相互独立．

    （1）求该网民分别购买两种商品的概率；

    （2）用随机变量表示该网民购买商品所享受的优惠券钱数，求的分布列．

    查看答案和解析>>

    同步练习册答案