
分析 (1)由已知利用二倍角的余弦函数公式可求cos2C=$\frac{3}{8}$,利用同角三角函数基本关系式即可求得sinC的值.
(2)由已知可求sinA=$\frac{\sqrt{10}}{8}$,由a2+b2<c2,可得C为钝角,解得cosC=-$\frac{\sqrt{6}}{4}$,利用正弦定理可得c的值,由余弦定理整理可得:b2+$\sqrt{6}$b-12=0,即可解得b的值.
解答 解:(1)在△ABC中,∵cos2C=2cos2C-1=-$\frac{1}{4}$,
∴解得:cos2C=$\frac{3}{8}$,
∴sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{10}}{4}$.
(2)∵a=2,sinC=$\frac{\sqrt{10}}{4}$,2sinA=sinC,
∴sinA=$\frac{\sqrt{10}}{8}$,
∵a2+b2<c2,可得C为钝角,cos2C=$\frac{3}{8}$,
∴cosC=-$\frac{\sqrt{6}}{4}$,
∴由正弦定理可得:c=$\frac{asinC}{sinA}$=$\frac{2×\frac{\sqrt{10}}{4}}{\frac{\sqrt{10}}{8}}$=4,
由余弦定理可得:c2=a2+b2-2abcosC,即:16=4+b2-2×2×b×(-$\frac{\sqrt{6}}{4}$),整理可得:b2+$\sqrt{6}$b-12=0,解得:b=$\sqrt{6}$,或-2$\sqrt{6}$(舍去).
点评 本题主要考查了二倍角的余弦函数公式,同角三角函数基本关系式,正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
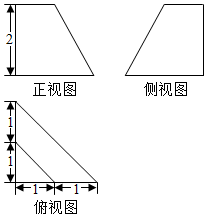
| A. | $\frac{7}{3}$ | B. | $\frac{17}{2}$ | C. | 13 | D. | $\frac{17+3\sqrt{10}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{1}{24}$ | D. | $\frac{15}{4}$ | ||||
| E. | $\frac{7}{3}$ | F. | $\frac{15}{4}$或$\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2x+1 | C. | 3+△x2 | D. | 3+△x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=$\sqrt{{x}^{2}-1}$,g(x)=$\sqrt{x+1}$•$\sqrt{x-1}$ | ||
| C. | f(x)=ln ex与g(x)=elnx | D. | f(x)=(x-1)0与g(x)=$\frac{1}{(x-1)^{0}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com