
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{3\sqrt{6}}{2}$ | D. | 2$\sqrt{6}$ |
分析 设出A,B,C点的坐标,再设出直线AB与x轴交于点D(m,0),进一步求出m,根据几何位置关系表示出三角形的面积,再根据导数知识求出最值,则答案可求.
解答 解:抛物线焦点坐标F(1,0),准线方程:x=-1
设A(x1,y1),B(x2,y2),C(x3,y3),直线AB与x轴交于点D(m,0),
∵$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}=\frac{0-{y}_{1}}{m-{x}_{1}}$,∴m=-$\frac{{y}_{1}{y}_{2}}{4}$
∵点F(1,0)满足$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,
∴点F是△ABC重心,
∴x1+x2+x3=3,y1+y2+y3=0,
∴y12+y22=12-y32,y1+y2=-y3,
∴2y1y2=(y1+y2)2-(y12+y22)=2y32-12
∴S△ABF2=$\frac{1}{4}$(1+$\frac{{y}_{1}{y}_{2}}{4}$)2(y1-y2)2=$\frac{1}{64}$(-$\frac{1}{2}$+$\frac{1}{4}$y32)2(24-3y32)
令y32=t≥0,y=(-2+t)2(8-t)
令y′=0,则t1=2,t2=6.
当t∈(0,2)时函数单调递减,当t∈(2,6)时函数单调递增,t∈(6,+∞)时函数单调递减且当t=0时y=$\frac{3}{2}$,当t=6时y=$\frac{3}{2}$,
∴ymax=$\frac{3}{2}$.
∴△ABF面积的最大值为$\frac{\sqrt{6}}{2}$.
故选:A.
点评 本题重点考查抛物线的简单性质,考查导数知识的运用,考查学生的计算能力,解题的关键是求出△ABF面积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
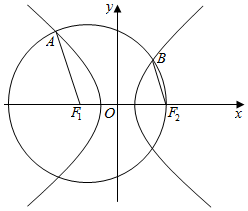 如图,设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,若以F1为圆心,以F1F2为半径的圆与C交于A,B两点(A在第二象限,B在第一象限),且F1A∥F2B,则双曲线C的离心率为( )
如图,设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,若以F1为圆心,以F1F2为半径的圆与C交于A,B两点(A在第二象限,B在第一象限),且F1A∥F2B,则双曲线C的离心率为( )| A. | $\frac{3+\sqrt{17}}{4}$ | B. | 2 | C. | $\frac{1+\sqrt{17}}{4}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | $\frac{7\sqrt{2}}{10}$ | D. | -$\frac{7\sqrt{2}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com