
【题目】已知四棱锥![]() 的底面为正方形,且该四棱锥的每条棱长均为
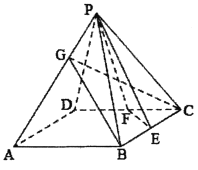
的底面为正方形,且该四棱锥的每条棱长均为![]() ,设BC,CD的中点分别为E,F,点G在线段PA上,如图.
,设BC,CD的中点分别为E,F,点G在线段PA上,如图.
(1)证明:![]() ;
;
(2)当![]() 平面PEF时,求直线GC和平面PEF所成角的正弦值.
平面PEF时,求直线GC和平面PEF所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() ,由正棱锥的性质可知PO⊥平面ABCD,得到PO⊥EF,再由ABCD是正方形结合EF为△BCD的中位线,可得EF⊥AC,得到EF⊥平面PAC,进一步得到EF⊥GC;
,由正棱锥的性质可知PO⊥平面ABCD,得到PO⊥EF,再由ABCD是正方形结合EF为△BCD的中位线,可得EF⊥AC,得到EF⊥平面PAC,进一步得到EF⊥GC;
(2)分别以PB,OC,OP为x,y,z轴建立空间直角坐标系,求出A,P,E,F的坐标,设![]() ,且
,且![]() ,其中
,其中![]() ,求得
,求得![]() ,设平面PEF的一个法向量为
,设平面PEF的一个法向量为![]() ,求得
,求得![]() ,结合BG∥平面PEF,利用数量积为0求得λ,进一步得到
,结合BG∥平面PEF,利用数量积为0求得λ,进一步得到![]() ,又
,又![]() ,求出直线GC的法向量为
,求出直线GC的法向量为![]() .设GC和平面PEF所成角为
.设GC和平面PEF所成角为![]() ,再由
,再由![]() 求解.
求解.
(1)证明:由已知![]() 为正四棱锥,设AC,BD交于点O,
为正四棱锥,设AC,BD交于点O,
由正棱锥的性质可知![]() 平面ABCD,所以
平面ABCD,所以![]() ,
,
由于正方形ABCD满足![]() ,EF为
,EF为![]() 的中位线,故
的中位线,故![]() ,所以
,所以![]() ,
,
所以![]() 平面PAC,而
平面PAC,而![]() 平面PAC,所以
平面PAC,所以![]() .
.
(2)分别以OB,OC,OP为坐标轴建立如图坐标系,
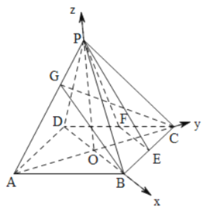
此时![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() ,且
,且![]() ,其中
,其中![]() ,
,
即![]() ,
,
设平面PEF的法向量为![]() ,
,
由于![]() ,
,![]() ,
,
由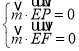 解得
解得![]() ,
,
由![]() 平面PEF知
平面PEF知![]() ,
,
解得![]() ,此时
,此时![]() ,由于
,由于![]() ,故
,故![]() .
.
所以直线GC的方向向量![]() ,
,
设GC和平面PEF所成角为![]() ,
,
则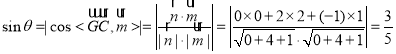 .
.


科目:高中数学 来源: 题型:
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
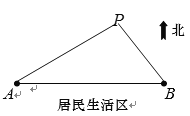
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,∠PAD=90°,CD∥AB,∠BAD=90°,且AB=3CD=3PA![]() AD=3.
AD=3.
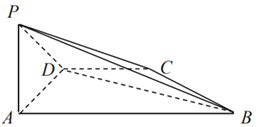
(1)求证:BD⊥PC;
(2)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了![]() ,
,![]() ,
,![]() ,
,![]() 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是![]() ,3号门里是
,3号门里是![]() ;乙同学说:2号门里是
;乙同学说:2号门里是![]() ,3号门里是
,3号门里是![]() ;丙同学说:4号门里是
;丙同学说:4号门里是![]() ,2号门里是
,2号门里是![]() ;丁同学说:4号门里是
;丁同学说:4号门里是![]() ,3号门里是
,3号门里是![]() .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为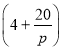 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com