
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,三角形VAB为等边三角形,AC⊥BC且 AC=BC= ![]() ,O、M分别为AB和VA的中点.
,O、M分别为AB和VA的中点. 
(1)求证:VB∥平面MOC;
(2)求直线MC与平面VAB所成角.
【答案】
(1)证明:∵O,M分别为AB,VA的中点,
∴VB∥OM,
又VB平面MOC,OM平面MOC,
∴VB∥平面MOC
(2)解:由题意,CO⊥AB,
∵平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,
∴CO⊥平面VAB,
∴∠CMO是直线MC与平面VAB所成角.
∵AC⊥BC且AC=BC= ![]() ,
,
∴CO= ![]() AB=1,
AB=1,
∵MO=1,
∴∠CMO=45°,
∴直线MC与平面VAB所成角是45°
【解析】(1)由中位线定理得VB∥OM,故而VB∥平面MOC;(2)证明∠CMO是直线MC与平面VAB所成角,即可得出结论.
【考点精析】通过灵活运用直线与平面平行的判定和空间角的异面直线所成的角,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则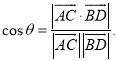 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)(ω>0,||< ![]() ,x∈R)的部分图象如图所示,则函数表达式为( )
,x∈R)的部分图象如图所示,则函数表达式为( ) 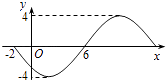
A.y=﹣4sin( ![]() )
)
B.y=4sin( ![]() )
)
C.y=﹣4sin( ![]() )
)
D.y=4sin( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
: 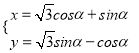 (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)曲线![]() 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线![]() 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
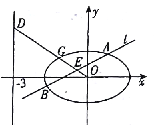
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如图).s1、s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( ) 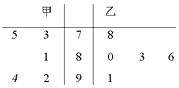
A.s1>s2
B.s1=s2
C.s1<s2
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】排列组合
(1)7位同学站成一排,甲、乙两同学必须相邻的排法共有多少种?
(2)7位同学站成一排,甲、乙和丙三个同学都不能相邻的排法共有多少种?
(3)7位同学站成一排,甲不站排头,乙不站排尾,不同站法种数有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足: ![]() (
(![]() )的数列
)的数列![]() 为“
为“![]() 级梦数列”.
级梦数列”.
(1)若![]() 是“
是“![]() 级梦数列”且
级梦数列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 级梦数列”且满足
级梦数列”且满足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0级梦数列”且
是“0级梦数列”且![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() .证明:
.证明: ![]() (
(![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com