
| x |
| 2 |
| x2 |
| C | r8 |
| x |
| 2 |
| x2 |
| C | r8 |
| 8-5r |
| 2 |
| 8-5r |
| 2 |
| 8-5r |
| 2 |
| C | r-18 |
| C | r8 |
| C | r+18 |
| 2 | r+1 |
|
| C | 58 |
| 17 |
| 2 |
| 17 |
| 2 |


科目:高中数学 来源:不详 题型:解答题
 月
月 日)将水果送到,则销售商一次性支付给果园20万元; 若在约定日期前送到,每提前一天销售商将多支付给果园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给果园1万元.
日)将水果送到,则销售商一次性支付给果园20万元; 若在约定日期前送到,每提前一天销售商将多支付给果园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给果园1万元.| 统计信息 汽车行驶路线 | 不堵车的情况下到达城市乙所需 时间(天) | 堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 |  |  |
| 公路2 | 1 | 4 |  |  |
 销售商支付给果园的费用
销售商支付给果园的费用 运费)
运费) (单位:万元),求
(单位:万元),求 的分布列和数学期望
的分布列和数学期望 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列及数学期望:
的分布列及数学期望:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
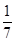 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com