
【题目】已知函数f(x)=logax,g(x)=m2x2﹣2mx+1,若b>a>1,且f(b)![]() ,ab=ba.
,ab=ba.
(1)求a与b的值;
(2)当x∈[0,1]时,函数g(x)的图象与h(x)=f(x+1)+m的图象仅有一个交点,求正实数m的取值范围.
【答案】(1)a=2,b=4.(2)(0,1]∪[3,+∞).
【解析】
(1)利用![]() 以及
以及![]() 列方程组,由此求解出
列方程组,由此求解出![]() 的值.
的值.
(2)首先求得![]() 、
、![]() 的单调区间,将
的单调区间,将![]() 分成
分成![]() 两种情况,结合
两种情况,结合![]() 与
与![]() 图象仅有一个交点进行分类讨论,由此求得
图象仅有一个交点进行分类讨论,由此求得![]() 的取值范围.
的取值范围.
(1)f(x)=logax,(a>1),
若b>a,且![]() ,
,
可得![]() 或
或![]() ,
,
因为b>a>1,所以logab>1,
所以logab=2,即a2=b,
因为ab=ba
所以![]() ,
,
所以a2=2a,
解之得a=2,b=4.
(2)因为m为正数,g(x)=m2x2﹣2mx+1=(mx﹣1)2为二次函数,
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数,
为增函数,
函数y=log2(x+1)+m 为![]() 上的增函数,
上的增函数,
分两种情况讨论:
①当0<m≤1 时,![]() ,在区间[0,1]上,y=(mx﹣1)2为减函数,值域为[(m﹣1)2,1],
,在区间[0,1]上,y=(mx﹣1)2为减函数,值域为[(m﹣1)2,1],
函数y=log2(x+1)+m 为增函数,值域为[m,m+1],此时两个函数图象有一个交点,符合题意;
②当m>1,得![]() ,在区间
,在区间![]() 上,y=(mx﹣1)2为减函数,在区间
上,y=(mx﹣1)2为减函数,在区间![]() 为增函数,
为增函数,
函数y=log2(x+1)+m 为增函数,值域为[m,m+1],
若两个函数图象有一个交点,则有(m﹣1)2≥m+1,解之得m≤0 或m≥3,
因为m为正数,则m≥3;
综上m的取值范围为(0,1]∪[3,+∞).


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的单调函数f(x),x∈(0,+∞),f[f(x)﹣lnx]=1,则方程f(x)﹣f′(x)=1的解所在区间是 ( )
A. (2,3) B. ![]() C.
C. ![]() D. (1,2)
D. (1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“人机大战,柯洁哭了,机器赢了”,2017年5月27日,![]() 岁的世界围棋第一人柯洁
岁的世界围棋第一人柯洁![]() 不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的
不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的![]() 男性中,有
男性中,有![]() 人持反对意见,
人持反对意见,![]() 名女性中,有
名女性中,有![]() 人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.分层抽样B.回归分析C.独立性检验D.频率分布直方图
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)过椭圆的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,其中直线
,其中直线![]() 交椭圆于
交椭圆于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于
于![]() 点,求证:直线
点,求证:直线![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是边长为2的正方形,SA=SB=SC=SD![]() ,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.
,点E,M,N分别是BC,CD,SC的中点,点P是MN上的一点.
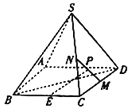
(1)证明:EP∥平面SBD;
(2)求四棱锥S﹣ABCD的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com