设函数fn(θ)＝sinnθ＋(－1)ncosnθ，0≤θ≤
，其中n为正整数．
(1)判断函数f1(θ)，f3(θ)的单调性，并就f1(θ)的情形证明你的结论；
(2)证明：2f6(θ)－f4(θ)＝(cos4θ－sin4θ)(cos2θ－sin2θ)．
解 (1)f1(θ)，f3(θ)在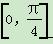
上均为单调递增函数．
对于函数f1(θ)＝sinθ－cosθ，设θ1<θ2，θ1，θ2∈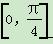，则f1(θ1)－f1(θ2)＝(sinθ1－sinθ2)＋(cosθ2－cosθ1)，
可得sinθ1<sinθ2，cosθ2<cosθ1，
∴f1(θ1)<f1(θ2)，函数f1(θ)在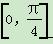上单调递增．
(2)证明：∵原式左边＝2(sin6θ＋cos6θ)－(sin4θ＋cos4θ)
＝2(sin2θ＋cos2θ)(sin4θ－sin2θ·cos2θ＋cos4θ)－(sin4θ＋cos4θ)
＝sin4θ－2sin2θcos2θ＋cos4θ＝(sin2θ－cos2θ)2＝cos22θ.
又∵原式右边＝(cos2θ－sin2θ)2＝cos22θ，
∴2f6(θ)－f4(θ)＝(cos4θ－sin4θ)(cos2θ－sin2θ)．
阅读快车系列答案科目：高中数学 来源： 题型：
已知数列{an}的前n项和为Sn满足：Sn＝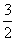
an＋n－3.
(1)求证：数列{an－1}是等比数列．
(2)令cn＝log3(a1－1)＋log3(a2－1)＋…＋log3(an－1)，对任意n∈N*，是否存在正整数m，使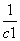
＋
＋…＋
≥
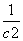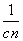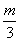都成立？若存在，求出m的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
观察下式：1＝12,2＋3＋4＝32,3＋4＋5＋6＋7＝52,4＋5＋6＋7＋8＋9＋10＝72，…，则第n个式子是( )
A．n＋(n＋1)＋(n＋2)＋…＋(2n－1)＝n2
B．n＋(n＋1)＋(n＋2)＋…＋(2n－1)＝(2n－1)2
C．n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2
D．n＋(n＋1)＋(n＋2)＋…＋(3n－1)＝(2n－1)2
查看答案和解析>>
科目：高中数学 来源： 题型：
平面中的三角形和空间中的四面体有很多相类似的性质，例如在三角形中，(1)三角形两边之和大于第三边；(2)三角形的面积S＝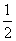
×底×高；(3)三角形的中位线平行于第三边且等于第三边的；…
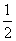请类比上述性质，写出空间中四面体的相关结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
对于不等式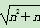
<n＋1(n∈N*)，某同学用数学归纳法的证明过程如下：
(1)当n＝1时，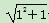
<1＋1，不等式成立．
(2)假设当n＝k(k∈N*且k≥1)时，不等式成立，即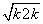
<k＋1，则当n＝k＋1时，
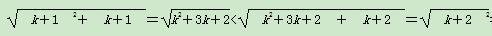＝(k＋1)＋1，
所以当n＝k＋1时，不等式成立，则上述证法( )
A．过程全部正确
B．n＝1验得不正确
C．归纳假设不正确
D．从n＝k到n＝k＋1的推理不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，且Sn＝n(2n－1)an，通过求a2，a3，a4，猜想an的表达式为( )
<loga