练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    观察下式：1＝12,2＋3＋4＝32,3＋4＋5＋6＋7＝52,4＋5＋6＋7＋8＋9＋10＝72，…，则第n个式子是(　　)

    A．n＋(n＋1)＋(n＋2)＋…＋(2n－1)＝n2

    B．n＋(n＋1)＋(n＋2)＋…＋(2n－1)＝(2n－1)2

    C．n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2

    D．n＋(n＋1)＋(n＋2)＋…＋(3n－1)＝(2n－1)2


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    数列{an}的首项为3，{bn}为等差数列，且bn＝an＋1－an(n∈N*)，若b3＝－2，b10＝12，则a8＝(　　)

    A．0                                    B．3

    C．8                                    D．11

    在递减等差数列{an}中，若a1＋a5＝0，则Sn取最大值时n等于(　　)

    A．2                                    B．3

    C．4                                    D．2或3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若数列{an}的通项为an＝4n－1，bn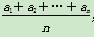＝，n∈N*，则数列{bn}的前n项和是(　　)

    A．n2                                   B．n(n＋1)

    C．n(n＋2)                              D．n(2n＋1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不相等的三个正数a，b，c成等差数列，并且x是a，b的等比中项，y是b，c的等比中项，则x2，b2，y2三数(　　)

    A．成等比数列而非等差数列

    B．成等差数列而非等比数列

    C．既成等差数列又成等比数列

    D．既非等差数列又非等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a、b是两个实数，给出下列条件：

    ①a＋b>1；②a＋b＝2；③a＋b>2；④a2＋b2>2；⑤ab>1.

    其中能推出：“a、b中至少有一个大于1”的条件是________(填序号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    观察下列图形中小正方形的个数，则第6个图中有__________个小正方形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数fn(θ)＝sinnθ＋(－1)ncosnθ，0≤θ≤，其中n为正整数．

    (1)判断函数f1(θ)，f3(θ)的单调性，并就f1(θ)的情形证明你的结论；

    (2)证明：2f6(θ)－f4(θ)＝(cos4θ－sin4θ)(cos2θ－sin2θ)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若a>b>0，则下列不等式不成立的是(　　)

    A.<                                 B．|a|>|b|

    C．a＋b<2                          D

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知0<a<1，若loga(2x－y＋1)<loga(3y－x＋2)，且λ<x＋y，则λ的最大值为________．

    查看答案和解析>>

    同步练习册答案