练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    数列{an}的首项为3，{bn}为等差数列，且bn＝an＋1－an(n∈N*)，若b3＝－2，b10＝12，则a8＝(　　)

    A．0                                    B．3

    C．8                                    D．11

    在递减等差数列{an}中，若a1＋a5＝0，则Sn取最大值时n等于(　　)

    A．2                                    B．3

    C．4                                    D．2或3


    　D


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在直角三角形ABC中，∠C＝，AC＝3，取点D使＝(　　)

    A．3                                    B．4

    C．5                                    D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，已知BD⊥AB于B，DC⊥AC于C，若DB=DC，AD=DG，∠BAC=40°，则∠ADG=　　．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列1，，，，，，，，，，…，则是此数列中的第________项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    古希腊人常用小石子在沙滩上摆成各种形状来研究数，如图所示．

    他们研究过图中的1,5,12,22，…，由于这些数能够表示成五角形，将其称为五角形数，若按此规律继续下去，第n个五角形数an＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和Sn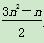＝，n∈N*.

    (1)求数列{an}的通项公式；

    (2)证明：对任意的n>1，都存在m∈N*，使得a1，an，am成等比数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    各项都为正数的等比数列{an}中，首项a1＝3，前三项和为21，则a3＋a4＋a5＝(　　)

    A．33                                   B．72

    C．84                                   D．189

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于函数y＝f(x)，部分x与y的对应关系如下表：

    x

    1

    2

    3

    4

    5

    6

    7

    8

    9

    y

    3

    7

    5

    9

    6

    1

    8

    2

    4

    数列{xn}满足x1＝1，且对任意n∈N*，点(xn，xn＋1)都在函数y＝f(x)的图象上，则x1＋x2＋x3＋x4＋…＋x2 013＋x2 014的值为(　　)

    A．7 549                                B．7 545

    C．7 539                                D．7 535

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    观察下式：1＝12,2＋3＋4＝32,3＋4＋5＋6＋7＝52,4＋5＋6＋7＋8＋9＋10＝72，…，则第n个式子是(　　)

    A．n＋(n＋1)＋(n＋2)＋…＋(2n－1)＝n2

    B．n＋(n＋1)＋(n＋2)＋…＋(2n－1)＝(2n－1)2

    C．n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2

    D．n＋(n＋1)＋(n＋2)＋…＋(3n－1)＝(2n－1)2

    查看答案和解析>>

    同步练习册答案