Question

【题目】如图，在平面直角坐标系xOy中，椭圆C： + =1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 点P（3，1）在椭圆上，△PF1F2的面积为2 ．
（1）①求椭圆C的标准方程； ②若∠F1QF2= ，求QF1QF2的值．
（2）直线y=x+k与椭圆C相交于A，B两点，若以AB为直径的圆经过坐标原点，求实数k的值．

Answer 1

【答案】
（1）解：①由条件，可设椭圆的标准方程为 ，将点P（3，1）代入椭圆方程，

∴ ，

由 = 2c1=2 ，即

又a2=b2+c2，

∴a2=12，b2=4，

∴椭圆的标准方程为： ；

②当 时，有

∴

（2）解：设A（x1，y1），B（x2，y2），由 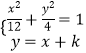，得4x2+6kx+3k2﹣12=0

由韦达定理及直线方程可知： ，

∵以AB为直径的圆经过坐标原点，则 ，

解得： ，此时△=120＞0，满足条件，

因此

【解析】（1）由三角形的面积 = 2c1，即可求得 ，将点P（3，1）代入椭圆方程，由椭圆的性质a2=b2+c2 ， 即可求得a和b的值，求得椭圆方程；当 时，根据椭圆的性质及完全平方公式，即可求得QF1QF2的值；（2）将直线方程代入椭圆方程，求得关于x的一元二次方程，由韦达定理求得x1x2及y1y2 ， 由题意可知 =0，根据向量数量积的坐标运算，即可求得实数k的值．