Question

【题目】如图，在多面体ABCDNPM中，底面ABCD是菱形，∠ABC＝60°，PA⊥平面ABCD，AB＝AP＝2，PM∥AB，PN∥AD，PM＝PN＝1.

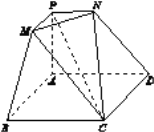
(1)求证：MN⊥PC；

(2)求平面MNC与平面APMB所成锐二面角的余弦值.

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：(1)先利用平行关系证明线线平行，利用菱形的对角线垂直、线面垂直的判定和性质进行证明；(2)建立适当的空间直角坐标系，写出相关点的坐标，求出有关直线的方向向量和平面的法向量，再利用空间向量的夹角公式进行求解.

试题解析：(1)证明：作ME∥PA交AB于E，NF∥PA交AD于F，连接EF，BD，AC.

由PM∥AB，PN∥AD，易得，所以四边形MEFN是平行四边形，

所以MN∥EF，因为底面ABCD是菱形，所以AC⊥BD，又易得EF∥BD，所以AC⊥EF，所以AC⊥MN，

因为PA⊥平面ABCD，EF平面ABCD，所以PA⊥EF，所以PA⊥MN，因为AC∩PA＝A，

所以MN⊥平面PAC，故MN⊥PC.

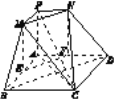
(2)建立空间直角坐标系如图所示，

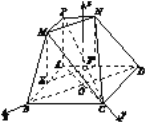
则C(0，1，0)，M，N，A(0，－1，0)，P(0，－1，2)，B(，0，0)，

所以＝，＝，＝(0，0，2)，＝(，1，0)，设平面MNC的法向量为m＝(x，y，z)，则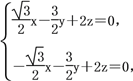令z＝1，得x＝0，y＝，所以m＝；

设平面APMB的法向量为n＝(x1，y1，z1)，则

令x1＝1，得y1＝－，z1＝0，所以n＝(1，－，0)，

设平面MNC与平面APMB所成锐二面角为α，

则cos α＝＝＝，

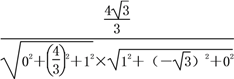所以平面MNC与平面APMB所成锐二面角的余弦值为.