练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某家具城进行促销活动，促销方案是：顾客每消费满1000元，便可以获得奖券一张，每张奖券中奖的概率为，若中奖，则家具城返还顾客现金1000元，某顾客购买一张价格为3400元的餐桌，得到3张奖券，设该顾客购买餐桌的实际支出为（元）；

    （1）求的所有可能取值；

    （2）求的分布列和数学期望；

    【答案】（1）见解析；（2）见解析

    【解析】

    （1）3张奖券中奖的可能情况为：没中奖、中奖1次、中奖2次和中奖3次，故可求出的所有可能取值；

    （2）根据的所有可能取值，求出相应的概率，即可得到概率分布列，从而可求数学期望.

    解：（1）3张奖券中奖的可能情况为：没中奖、中奖1次、中奖2次和中奖3次，

    的所有可能取值为3400，2400，1400，400 ；

    （2）

    的分布列为

    3400

    2400

    1400

    400

    P

    数学期望

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=sinxcosx﹣ x．
    （Ⅰ）求f（x）的最小正周期；
    （Ⅱ）当x∈[0， ]时，求f（x）的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着网络时代的进步，流量成为手机的附带品，人们可以利用手机随时随地的浏览网页，聊天，看视频，因此，社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查，所得结果统计如下图所示：

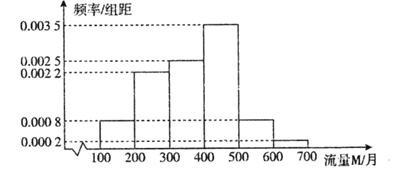
    （Ⅰ)以频率估计概率，若在该地区任取3位居民，其中恰有位居民的月流量的使用情况

    在300M∽400M之间，求的期望；

    （Ⅱ）求被抽查的居民使用流量的平均值；

    （Ⅲ）经过数据分析，在一定的范围内，流量套餐的打折情况与其日销售份数成线性相关

    关系，该研究人员将流量套餐的打折情况与其日销售份数的结果统计如下表所示：

    折扣

    1折

    2折

    3折

    4折

    5折

    销售份数

    50

    85

    115

    140

    160

    试建立关于的的回归方程.

    附注：回归方程中斜率和截距的最小二乘估计公式分别为：

    ，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的前n项和为Sn，a3=7，S9=27．

    （1）求数列{an}的通项公式；

    （2）若bn=|an|，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中正确的是（ ）
    A.若ξ服从正态分布N（0，2），且P（ξ＞2）=0.4，则P（0＜ξ＜2）=0.2
    B.x=1是x2﹣x=0的必要不充分条件
    C.直线ax+y+2=0与ax﹣y+4=0垂直的充要条件为a=±1
    D.“若xy=0，则x=0或y=0”的逆否命题为“若x≠0或y≠0，则xy≠0”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，其中左焦点(-2,0).

    （1） 求椭圆C的方程；

    （2） 若直线y=x+m与椭圆C交于不同的两点A，B，且线段AB的中点M在圆x2+y2=1上，求m的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）证明：；

    （2）若对任意，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{an}是递增的等差数列，且满足a2a4=21，a1+a5=10．

    （1）求{an}的通项公式；

    （2）若数列{cn}前n项和Cn=an+1，数列{bn}满足bn=2ncn（n∈N*），求{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设关于某种设备的使用年限 (年)与所支出的维修费用 (万元)有如下统计资料：

    x

    2

    3

    4

    5

    6

    y

    2.2

    3.8

    5.5

    6.5

    7.0

    已知， .

    ，

    (1)求， ；

    (2)若 与具有线性相关关系，求出线性回归方程；

    (3)估计使用年限为10年时，维修费用约是多少？

    查看答案和解析>>

    同步练习册答案