
已知曲线 y = x3 + x-2 在点 P0 处的切线 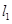 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线 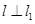 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
(1) (-1,-4);(2) 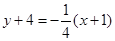 即
即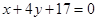 .
.
解析试题分析:(1)根据曲线方程求出导函数,因为已知直线4x-y-1=0的斜率为4,根据切线与已知直线平行得到斜率相等都为4,所以令导函数等于4得到关于x的方程,求出方程的解,即为切点P0的横坐标,代入曲线方程即可求出切点的纵坐标,又因为切点在第3象限,进而写出满足题意的切点的坐标;
(2)根据两直线垂直,斜率乘积为-1,可求出直线l的斜率为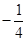 ,再根据点斜式,即可求出答案.
,再根据点斜式,即可求出答案.
试题解析:解:⑴由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.当x=1时,y=0;当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为 (-1,-4) .5分
⑵∵直线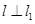 ,
,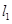 的斜率为4,∴直线l的斜率为
的斜率为4,∴直线l的斜率为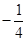 ,
,
∵l过切点P0,点P0的坐标为 (-1,-4)
∴直线l的方程为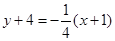 即
即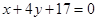 10分
10分
考点:1.导数在切线中的应用;2.直线的方程.


科目:高中数学 来源: 题型:解答题
已知函数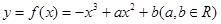
(1)若函数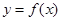 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数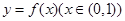 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求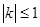 的充要条件;
的充要条件;
(3)若函数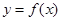 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件,每日产品废品率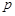 与日产量
与日产量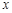 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率
(日产品废品率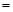
 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润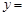 日正品赢利额
日正品赢利额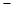 日废品亏损额)
日废品亏损额)
(1)将该车间日利润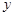 (千元)表示为日产量
(千元)表示为日产量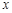 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某工厂生产 件产品的成本为
件产品的成本为 (元),
(元),
问:(1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;
(2)求函数 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线 与曲线
与曲线 没有公共点,求
没有公共点,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com